Задача D. Кольцевая автодорога ≡
| Автор: | Центральная предметно-методическая комиссия по информатике | Ограничение времени: | 2 сек | |
| Входной файл: | road.in | Ограничение памяти: | 64 Мб | |
| Выходной файл: | road.out | |||
| Максимальный балл: | 100 |
Условие
К 2110 году город Флэтбург, являясь одним из крупнейших городов мира, не имеет обходной автомагистрали, что является существенным препятствием для его развития как крупнейшего транспортного центра мирового значения. В связи с этим еще в 2065 году при разработке Генерального плана развития Флэтбурга была определена необходимость строительства кольцевой автомобильной дороги.
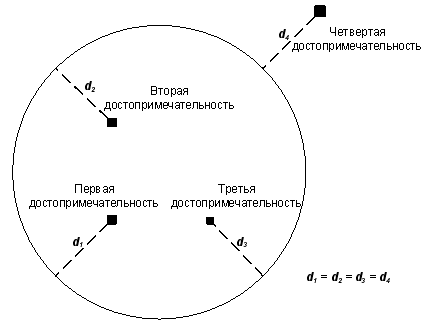
В Генеральном плане также были обозначены требования к этой дороге. Она должна соответствовать статусу кольцевой — иметь форму окружности. Кроме этого, четыре крупные достопримечательности Флэтбурга должны быть в одинаковой транспортной доступности от дороги. Это предполагается обеспечить тем, что они будут находиться на равном расстоянии от нее. Расстоянием от точки расположения достопримечательности до дороги называется наименьшее из расстояний от этой точки до некоторой точки, принадлежащей окружности автодороги.
Дирекция по строительству города Флэтбурга, ответственная за постройку кольцевой автодороги, решила привлечь передовых программистов для выбора оптимального плана постройки дороги.
Требуется написать программу, которая вычислит число возможных планов постройки кольцевой автомобильной дороги с соблюдением указанных требований и найдет такой план, для которого длина дороги будет минимальной.
Формат входного файла
Входной файл содержит четыре строки. Каждая из них содержит по два целых числа: xi и yi — координаты места расположения достопримечательности. Первая строка описывает первую достопримечательность, вторая — вторую, третья — третью, четвертая — четвертую. Никакие две достопримечательности не находятся в одной точке.
Формат выходного файла
В первой строке выходного файла требуется вывести число возможных планов постройки кольцевой автомобильной дороги. Если таких планов бесконечно много, необходимо вывести в первой строке выходного файла слово Infinity.
На второй строке требуется вывести координаты центра дороги минимальной длины и ее радиус. Если существует несколько разных способов построения дороги минимальной длины, необходимо вывести координаты центра и радиус любой из них. Координаты центра и радиус дороги должны быть выведены с точностью не хуже 10 − 8 и не превосходить по абсолютной величине 109.
Ограничения
− 100 ≤ xi, yi ≤ 100
Примеры тестов
| № | Входной файл (road.in) |
Выходной файл (road.out) |
|---|---|---|
| 1 | |
|
| 2 | |
|