Problem D. Dragon claw ≡
| Author: | G. Grenkin | Time limit: | 1 sec | |
| Input file: | input.txt | Memory limit: | 256 Mb | |
| Output file: | output.txt |
Statement
 A sculpture of dragon is established in the campus of Far Eastern Federal University.
There are long claws on dragon's paws.
According to a legend, when a student passes the session successfully,
the claws grow a little (by several nanometers).
That's why students took an interest how much the area of the claw
will increase when the claw grows by d mm.
A sculpture of dragon is established in the campus of Far Eastern Federal University.
There are long claws on dragon's paws.
According to a legend, when a student passes the session successfully,
the claws grow a little (by several nanometers).
That's why students took an interest how much the area of the claw
will increase when the claw grows by d mm.
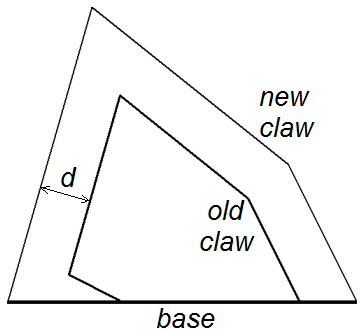
Students constructed the following mathematical model of dragon's claw growth. The claw has the shape of a convex polygon with a base on the abscissa axis. The claw grows equally in all directions and doesn't grow below its base. When the claw grows by d mm, all its sides shift in parallel by d mm to the outside (see the figure). The base of the claw remains at the same place, so one should intersect the new polygon with the abscissa axis.
Your program must calculate the area of the claw before and after its growing.
Input file format
Input file contains integers N d, followed by N pairs of integers xi yi — coordinates of vertices of the polygon in millimeters in the clockwise order. The polygon is non-degenerate.
Output file format
Output file must contain 2 real numbers: the area of the claw before and after growing in mm2 with at least 4 correct digits after the decimal point.
Constraints
3 ≤ N ≤ 40; 1 ≤ d ≤ 100; − 100 ≤ xi ≤ 100; 0 ≤ yi ≤ 100; y1 = yn = 0.
Sample tests
| No. | Input file (input.txt) |
Output file (output.txt) |
|---|---|---|
| 1 | |
|
| 2 | |
|