Задача 4. Полезные ископаемые ≡
| Автор: | Центральная предметно-методическая комиссия | Ограничение времени: | 1 сек | |
| Входной файл: | mining.in | Ограничение памяти: | 256 Мб | |
| Выходной файл: | mining.out | |||
| Максимальный балл: | 100 |
Условие
Ведется проект по освоению планеты соседней звездной системы. Для добычи полезных ископаемых планируется направить на планету несколько партий роботов.
Участок поверхности планеты, на котором планируется добывать полезные ископаемые, представляет собой клетчатый прямоугольник размером w на h, клетки участка имеют координаты от (1, 1) до (w, h). В некоторых клетках участка находятся базы специалистов, в которые могут быть доставлены партии роботов. Всего на участке размещено s баз, и i-я база находится в клетке с координатами (xi, yi).
Каждая партия роботов характеризуется тремя параметрами: j-я партия доставляется на базу bj, содержит nj роботов и каждый робот партии обладает мобильностью mj.
Когда партия роботов доставляется на соответствующую базу, каждый робот этой партии перемещается по поверхности планеты от базы до некоторой клетки. Если мобильность робота равна m, он может не более m раз переместиться на одну из восьми соседних клеток, как показано на рис. 1.
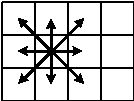
Рис. 1. Возможные перемещения робота в восьми направлениях.
После того как роботы из всех доставленных партий размещаются на участке, они активируются и начинают добычу полезных ископаемых. В процессе перемещения в одной клетке может одновременно находиться произвольное количество роботов. Однако после активации в каждой клетке должно находиться не более q роботов.
Руководством проекта получена информация о t партиях роботов, которые могут быть последовательно отправлены на планету. После доставки всех партий роботов, учитывая их ограниченную мобильность, возможна ситуация, что не удастся разместить роботов на участке так, чтобы в каждой клетке оказалось не больше q роботов. Поэтому руководство должно выбрать k первых партий роботов, где 0 ≤ k ≤ t, которые будут полностью доставлены на соответствующие базы. После этого, если k < t, следует дополнительно принять z из nk + 1 роботов следующей, (k + 1)-й партии, 0 ≤ z < nk + 1.
Все полученные таким образом роботы должны с учетом ограничения на мобильность разместиться на участке таким образом, чтобы в каждой клетке было не более q роботов. После этого они будут активированы и начнут добычу полезных ископаемых. Разумеется, руководство проекта старается максимизировать количество роботов, которые будут доставлены на планету, поэтому, с учетом описанных ограничений, требуется максимизировать k, а затем максимизировать z.
Требуется написать программу, которая по размерам участка, числу q, описанию расположения баз, а также количеству запланированных партий роботов и их описанию определяет максимальное число k — количество партий роботов, и затем – максимальное число z – дополнительное количество роботов из (k + 1)-й партии, чтобы, доставив роботов на планету, их можно было разместить на участке таким образом, чтобы в каждой клетке оказалось не более q роботов.
Формат входного файла
Первая строка входного файла содержит числа w, h, s и q. Последующие s строк содержат по два целых числа xi, yi и описывают базы специалистов (1 ≤ xi ≤ w, 1 ≤ yi ≤ h).
Следующая строка содержит число t — количество партий роботов. Последующие t строк описывают партии роботов и содержат по 3 целых числа: bj, nj и mj (1 ≤ bj ≤ s, 1 ≤ nj ≤ w × h × q, 0 ≤ mj < max(w, h)).
Формат выходного файла
Требуется вывести два числа: k и z, 0 ≤ k ≤ t. Если k = t, то z должно быть равно 0, иначе должно выполняться условие 0 ≤ z < nk + 1.
Ограничения
1 ≤ w, h ≤ 105, 1 ≤ s ≤ 4, 1 ≤ q ≤ 100, 1 ≤ t ≤ 100,
Пояснение к примеру
В приведенном примере описания входных данных следует полностью принять первую партию роботов и дополнительно принять 7 роботов из второй партии. На рис. 2 показано, как можно разместить этих роботов на участке, чтобы в каждой клетке было не более одного робота. Базы специалистов показаны кружками. Клетки, в которых окажутся роботы с базы 1, показаны вертикальной штриховкой, а клетки, в которых окажутся роботы с базы 2, показаны серым цветом.
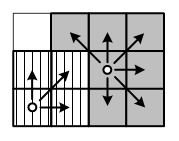
Рис. 2. Возможное размещение роботов на участке в данном примере.
Описание подзадач и системы оценивания
Баллы за каждую из подзадач 1–5 начисляются только в случае, если все тесты этой подзадачи и необходимых подзадач успешно пройдены.
Тесты для подзадачи 6 запускаются только в случае, если все тесты подзадач 1–5 успешно пройдены. Каждый тест в подзадаче 6 оценивается независимо в 1 балл.
| Подзадача | Баллы | Дополнительные ограничения | Необходимые подзадачи | ||
|---|---|---|---|---|---|
| w, h | s | q | |||
| 1 | 18 | 1 ≤ w, h ≤ 20 | s = 1 | q = 1 | |
| 2 | 12 | 1 ≤ w, h ≤ 20 | 1 ≤ s ≤ 2 | q = 1 | 1 |
| 3 | 9 | 1 ≤ w, h ≤ 20 | 1 ≤ s ≤ 3 | q = 1 | 1, 2 |
| 4 | 10 | 1 ≤ w, h ≤ 20 | 1 ≤ s ≤ 3 | 1 ≤ q ≤ 100 | 1, 2, 3 |
| 5 | 15 | 1 ≤ w, h ≤ 105 | s = 1 | 1 ≤ q ≤ 100 | 1 |
| 6 | 36 | 1 ≤ w, h ≤ 105 | 1 ≤ s ≤ 4 | 1 ≤ q ≤ 100 | 1, 2, 3, 4, 5 |
Получение информации о результатах окончательной проверки
По запросу сообщаются баллы за каждую подзадачу.
Примеры тестов
| № | Входной файл (mining.in) |
Выходной файл (mining.out) |
|---|---|---|
| 1 | |
|