Задача D. Учебники на полке ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 64 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
В кабинете математики ведется преподавание с 1 по k-й класс. На полке расположилось p комплектов учебников в следующем порядке: сначала p учебников за 1-й класс, потом p учебников за 2-й класс, ..., в самом конце p учебников за k-й класс.
Для развития устного счета учительница просит ребят определить количество способов выбрать несколько (не менее одного) учебников, стоящих подряд, таким образом, чтобы сумма чисел (номеров классов на корешках) равнялась бы n.
Формат входных данных
Три строки входного файла содержат три натуральных числа: k, p и n.
Формат выходных данных
Выведите одно неотрицательное целое число — ответ на вопрос задачи.
Ограничения
1 ≤ n ≤ 109
1 ≤ k × p ≤ 105
Система оценки и описание подзадач
Баллы за каждый тест начисляются независимо.
Решения, верно работающие при n = 1, получат не менее 10 баллов.
Решения, верно работающие при k = 1, получат не менее 10 баллов.
Решения, верно работающие при p = 1, n = k × (k + 1)2, получат не менее 10 баллов.
Решения, верно работающие при k × p ≤ 100, получат не менее 30 баллов.
Пояснения к примерам
Смотри рисунок. В обоих примерах три комплекта учебников с первого по восьмой класс.
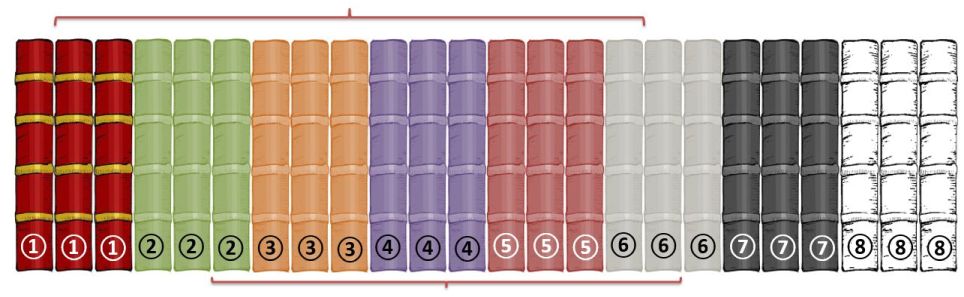
В первом примере требуется набрать сумму n = 5. Сделать это можно шестью способами:
1) 1 + 1 + 1 + 2;
2) 1 + 2 + 2;
3) 2 + 3;
4-6) выбрать любой из трех учебников за пятый класс.
Во втором примере требуется набрать сумму n = 50. Сделать это можно двумя способами, приведенными на рисунке.
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|
| 2 | |
|