Задача 2. Разделение прямоугольника ≡
| Входной файл: | Стандартный вход | Ограничение времени: | 1 сек | |
| Выходной файл: | Стандартный выход | Ограничение памяти: | 512 Мб | |
| Максимальный балл: | 100 |
Условие
Аня играет в новую настольную игру «Клетчатое королевство».
Рассмотрим прямоугольное клетчатое поле размером a × b.
Необходимо разделить его на m прямоугольников вертикальными или горизонтальными разрезами. Прямоугольники не обязательно должны получиться равными. Необходимо суммарно провести ровно k разрезов.
Каждый разрез представляет собой прямую линию от одного края поля до другого края поля. Разрезы разрешено делать только по границам клеток — линиям сетки.
Выведите, сколько провести горизонтальных (0 ≤ h < a) и сколько вертикальных (0 ≤ v < b) разрезов. Если поле можно разрезать несколькими способами, выведите тот, в котором горизонтальных разрезов меньше. Если поле нельзя разрезать требуемым образом, выведите − 1.
Формат входных данных
В первой строке дано ровно одно целое число t — количество тестов.
В следующих t строках находится описание тестов: в i-й строке через пробел даны четыре целых числа: a, b, k, m — высота и ширина поля, количество разрезов и количество прямоугольников соответственно.
Формат выходных данных
Для каждого теста выведите через пробел ровно два целых числа h и v — количество горизонтальных и количество вертикальных разрезов, если прямоугольное клетчатое поле можно разрезать требуемым образом, в противном случае выведите число − 1.
Ограничения
1 ≤ t ≤ 100
1 ≤ a, b ≤ 109, 0 ≤ k ≤ 2 ⋅ 109, 1 ≤ m ≤ 1018, k < m
Система оценки
Баллы за каждую подзадачу начисляются только в случае, если все тесты для этой подзадачи и необходимых подзадач успешно пройдены.
| Подзадача | Баллы | Дополнительные ограничения | Необходимые подзадачи | Информация о проверке |
|---|---|---|---|---|
| 1 | 18 | a = 1 | первая ошибка | |
| 2 | 19 | 1 ≤ m ≤ 105 | первая ошибка | |
| 3 | 20 | 1 ≤ k ≤ 105 | 2 | первая ошибка |
| 4 | 21 | 1 ≤ m ≤ 109 | 2 | первая ошибка |
| 5 | 22 | нет | 1 − 4 | первая ошибка |
Пояснение к примеру
В приведенном примере содержится три теста:
- В первом тесте поле можно разрезать, как показано на рисунке:
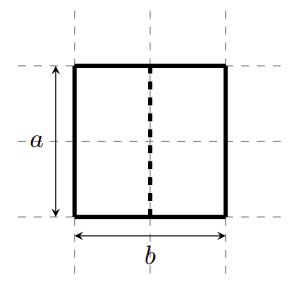
Иллюстрация к первому тесту:
a = 2, b = 2, k = 1, m = 2.
- Во втором тесте поле нельзя разрезать требуемым образом.
- В третьем тесте поле можно разрезать, как показано на рисунке:
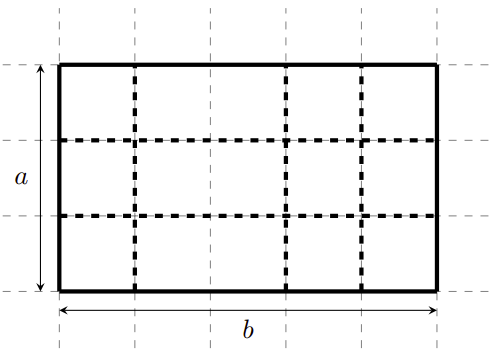
Иллюстрация к третьему тесту:
a = 3, b = 5, k = 5, m = 12.
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|
Разбор
Автор задачи: Андрей Станкевич
Пусть было проведено x горизонтальных и y вертикальных разрезов (0 ≤ x < a, 0 ≤ y < b).
Подзадача 1
Так как по условию подзадачи a = 1, то единственно возможное количество горизонтальных разрезов x = 0. Тогда количество вертикальных разрезов y = k. Остается проверить: если выполняются условия k < b и m = k + 1, то можно провести x = 0 горизонтальных и y = k вертикальных разрезов так, чтобы получилось ровно m = k + 1 частей, в противном случае поле нельзя разрезать требуемым образом.
Асимптотика такого решения O(1).
Подзадачи 2 и 3
Переберем возможное количество горизонтальных разрезов x (0 ≤ x ≤ k), по возрастанию. Вычислим количество вертикальных разрезов y = k − x. Заметим, что если мы провели ровно x горизонтальных и ровно y вертикальных разрезов, то поле разделилось на p = (x + 1) ⋅ (y + 1) частей. Остается проверить: если p = m, то поле можно разрезать требуемым образом и мы нашли ответ {x, y}. Если для всех возможных x верно что p ≠ m, то поле нельзя разрезать требуемым образом.
Асимптотика такого решения O(k).
Подзадача 4
Аналогично предыдущей подзадаче хотим перебирать возможное количество горизонтальных разрезов x (0 ≤ x ≤ k). Будем делать это с учетом того, что число m должно делится на число x + 1. Для этого будем перебирать все делители числа m: пусть g — делитель числа m, тогда x = g − 1.
Асимптотика такого решения O(√m), так как чтобы перебрать все делители g числа m, достаточно перебирать их до корня (g ≤ √m).
Подзадача 5
Составим следующие уравнения: {x + y = k(x + 1) ⋅ (y + 1) = m
Выразим переменную y = k − x из первого уравнения и подставим во второе, получим: (x + 1) ⋅ (k − x + 1) = m
Раскроем скобки и приведем к стандартному виду: x ⋅ k − x2 + x + k − x + 1 = m − 1 ⋅ x2 + k ⋅ x + (k − m + 1) = 0
Это квадратное уравнение относительно переменной x вида: A ⋅ x2 + B ⋅ x + C = 0 где коэффициенты равны соответственно A = − 1, B = k, C = k − m + 1.
Вычислим дискриминант квадратного уравнения по известной формуле: D = B2 − 4 ⋅ A ⋅ C = k2 − 4 ⋅ ( − 1) ⋅ (k − m + 1) = k2 + 4 ⋅ (k − m + 1)
Если полученный дискриминант меньше нуля D < 0 или не существует целого числа q, такого что выполняется равенство q2 = D, то значит поле нельзя разрезать требуемым образом.
В противном случае вычислим целое число q = √D, а затем найдем два решения квадратного уравнения x1 и x2, и соответствующие им y1, y2: x1 = − B − √D2 ⋅ A = k + q2, y1 = k − x1 x2 = − B + √D2 ⋅ A = k − q2, y2 = k − x2.
Остается проверить, какое из решений {xi, yi}, где i = {1, 2}, подходит под ограничения: 0 ≤ xi < a и 0 ≤ yi < b и xi, yi ∈ Z и выбрать его в ответ. В случае, если под ограничение подходят оба решения, необходимо выбрать в ответ то из них, где количество горизонтальных разрезов xi минимально.
Асимптотика такого решения O(1).