Problem D. Distribution by desks ≡
| Author: | Евгений Татаринов, Антон Карабанов | Time limit: | 1 sec | |
| Input file: | Standard input | Memory limit: | 256 Mb | |
| Output file: | Standard output |
Statement
To conduct a mathematics Olympiad for grades 8 − 11, several classrooms have been allocated. The first classroom contains n rows of desks, with each row having 3 desks. Each desk accommodates exactly one person.
The organizers aim to seat students at all desks in the first classroom in such a way that in any 2 × 2 square of desks, students from different grades sit pairwise (meaning, in any square, there is one student from each of the 8th, 9th, 10th, and 11th grades).
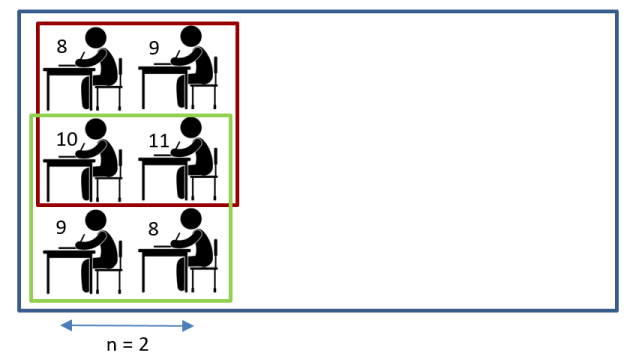
In the illustration, you can see one of the suitable seating arrangements for n = 2 (in both the red and green squares, students from different grades are seated).
How many different ways exist to arrange the participants, given that the total number of students in any grade is greater than the number of desks in the first classroom?
Input format
The only input line contains a natural number n.
Output format
Output a single natural number — the answer to the problem's question modulo 109 + 7 (since the number can be very large).
Constraints
1 ≤ n ≤ 1018
Sample tests
| No. | Standard input | Standard output |
|---|---|---|
| 1 | |
|
Explanation
Будем вместо чисел использовать буквы.
Определим для n = 1 количество различных рассадок. Они бывают двух типов:
a
b
a
верхняя и нижняя буквы совпадают, их будет 12 (среднюю букву мы выбираем 4 способами, первую и третью - 3) и
a
b
c
все буквы различны, их будет 24 (верхнюю букву мы выбираем 4 способами, вторую - 3 и третью - 2).
В первом случае есть две возможности продолжить рассадку:
a c | a d
b d | b c
a c | a d
Причём опять мы имеем рассадку, где верхняя и нижняя буквы совпадают.
Во втором случае есть единственная возможность продолжить рассадку
a c
b d
c a
Причём опять мы имеем рассадку, где все буквы различны.
Тогда ответ будет равен 12 * 2n − 1 + 24
По малой теореме Ферма, ap − 1 = 1 по модулю p для простого p. n − 1 = k по модулю p − 1, тогда 2n − 1 = 2k по модулю p, тогда 12 * 2n − 1 + 24 = 12 * 2k + 24 по модулю p. В нашем случае p = 109 + 7, что является простым числом. Осталось научиться быстро находить 2k по модулю p, что можно сделать с помощью алгоритма быстрого возведения в степень.