Задача B. Большой куш Бендера ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 256 Мб | |
| Выходной файл: | Стандартный выход |
Условие
и увеличим население Чебоксар до
семи тысяч семисот четырех человек.
А? Это будет очень эффектно...
Откроем "Пти-шво" и с этого "Пти-шво"
будем иметь верный гран-кусок хлеба...
Пти-шво (фр. маленькие лошадки) — старинная настольная азартная игра, появившаяся в Европе в XVIII веке. Игра представляла собой своеобразную имитацию скачек на ипподроме: пронумерованные рысаки, прикрепленные к спицам рулетки, вращались по кругу. На таких искусственных лошадей игроками делались ставки. Победителем становился тот из игроков, чья лошадь останавливалась на отметке «Финиш».

В организованном Остапом Бендером подпольном игровом клубе, каждый вечер собираются любители азартных развлечений. Жемчужиной заведения по праву считается копия московского ипподрома с движущимися по кругу игрушечными лошадками. Всего их n и каждая обладает своей угловой скоростью di, позволяющей ей за 1 секунду перемещаться по дуге di°.
Перед стартом все лошадки выстраиваются в прямую линию и одновременно начинают движение с постоянной скоростью (у каждой лошадки своя скорость). Ровно через t секунд все бегуны останавливаются. Выигрывает та лошадка, для которой угловое расстояние от неё до линии старта (но не наоборот) окажется наименьшим.
Формат входных данных
Первая строка входных данных содержит натуральное число n — количество скакунов, вторая — натуральное число t — время забега. В следующих n строках расположены различные натуральные числа di — угловые скорости лошадок.
Формат выходных данных
Выведите одно натуральное число — порядковый номер лошадки, оказавшейся ближе остальных к линии старта-финиша. Гарантируется, что входные данные таковы, что ответ окажется единственным. Для определённости считайте, что если рысак остановился точно на линии, то он победил.
Ограничения
2 ≤ n ≤ 359
1 ≤ t ≤ 109
1 ≤ di ≤ 359
Пояснение к примеру
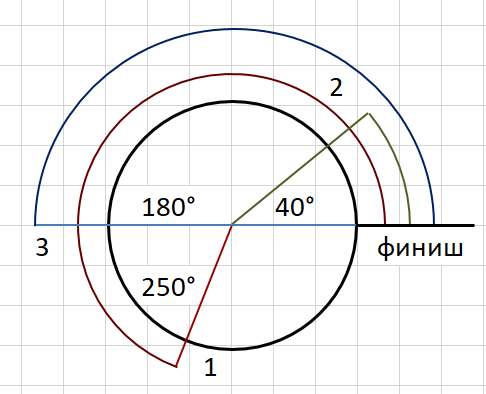
В примере дано три лошадки. Забег длится 10 секунд, угловые скорости бегунов 25, 40 и 90 соответственно. Смотри рисунок. На момент окончания забега первой лошади до линии финиша останется пробежать дугу 360° − 10 × 25° = 110°. Вторая лошадка сделает один полный круг и остановится на расстоянии до финиша 320°. Третья сделает два полных круга и остановится точно на середине дорожки (180°). Победит первая лошадь, для неё угловое расстояние до финиша наименьшее.
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|
Разбор
Целочисленное деление, поиск максимума.
Для каждой лошадки вычислим её конечное положение по формуле hi = di * t по модулю 360.
Среди всех hi найдём наибольшее (при этом считая, что hi = 0 больше всех).