Задача F. Ехидный барин ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 256 Мб | |
| Выходной файл: | Стандартный выход |
Условие
При проведении крестьянской реформы 1861 года и в соответствии с её «Общим положением о вышедших из крепостной зависимости», помещики обязаны были предоставить в пользование крестьянам полевой надел. Особенностью реформы было то, что земли надела предоставлялись не лично конкретному крестьянину, а в коллективное пользование сельским обществам, которые уже могли распределять их между хозяйствами по своему усмотрению.
Сельскому обществу надлежит распределить между хозяйствами полевой надел в форме квадрата со стороной n. По прихоти барина от двух противоположных углов квадрата следует отрезать два квадрата меньших размеров, чтобы их суммарная площадь равнялась площади оставшейся части, а всего получилось три земельных участка. Помогите крестьянам выполнить задание сумасбродного помещика.
Формат входных данных
Единственная строка входных данных содержит натуральное числа n. Гарантируется четность n.
Формат выходных данных
Выведите в первой строке натуральное число a — количество подходящих решений. В следующих a строках через пробел в порядке возрастания выведите два натуральных числа: стороны подходящих квадратных участков меньших размеров. Гарантируется, что входные данные предусматривают по крайней мере одно решение в натуральных числах. Пары выводите в порядке возрастания первого их двух чисел.
Ограничения
10 ≤ n ≤ 105
Пояснение к примерам
В первом примере дано n = 10. Смотри рисунок: единственное подходящее решение — отрезать от одного угла квадрат площадью 49, а от другого площадью 1. Тогда суммарная площадь двух квадратов равна 50 и равна площади оставшейся части. Решение, при котором отрезаются квадраты площадью 25 не подходит — большой квадрат разделится на четыре части, а не на три.
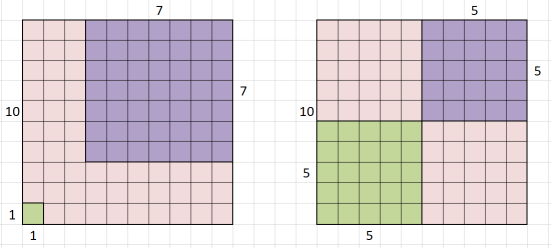
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|
| 2 | |
|
Разбор
Два указателя.
Заведём массив квадратов натуральных чисел от 1 до n: L = [i ** 2 for i in range(1, n + 1)]
Инициализируем 2 указателя: left = 0 и right = n - 1
Пока указатели не сошлись на расстояние равное 1, определяем суммарную площадь квадратов на которые указывают указатели.
Если 2 * (L[right] + L[left]) равно n ** 2, то мы нашли ещё одно решение, запоминаем его и сдвигаем оба указателя навстречу друг другу.
Если 2 * (L[right] + L[left]) меньше n ** 2, то левого указателя невозможно подобрать никакой подходящий правый. Увеличиваем левый указатель на 1.
Если 2 * (L[right] + L[left]) больше n ** 2, то правого указателя невозможно подобрать никакой подходящий левый. Уменьшаем правый указатель на 1.
В конце работы выводим все найденные решения.