Задача H. Забавная игра ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 256 Мб | |
| Выходной файл: | Стандартный выход |
Условие
Классики — старинная детская игра, популярная во всём мире. Одной из разновидностей правил являются следующие: на асфальт наносятся прямоугольники, как на рисунке ниже. Каждый участник совершает прыжки: сначала одной ногой на любое из двух полей по своему выбору, то есть на 1 или на 2, потом обеими ногами на поле с номером 3. Затем опять одной ногой на любое из двух полей по своему выбору, то есть на 4 или на 5, потом обеими ногами на поле с номером 6 и так далее. Остановиться можно в любой момент, а задача — набрать в сумме полей, на которые пришлись прыжки, ровно n.

Для указанного n определите количество различных подходящих маршрутов.
Формат входных данных
Единственная строка входных данных содержит натуральное число n.
Обратите внимание, что при заданных ограничениях для хранения ответа необходимо использовать 64-битный тип данных, например long long в C++, int64 в Free Pascal, long в Java.
Формат выходных данных
Выведите одно неотрицательное целое число — ответ на вопрос задачи.
Ограничения
1 ≤ n ≤ 10000
Пояснения к примерам
Сумму 22 в первом примере можно набрать тремя способами:
- 1 + 3 + 4 + 6 + 8;
- 1 + 3 + 5 + 6 + 7;
- 2 + 3 + 4 + 6 + 7.
Сумму 3 во втором примере набрать не получится: после первого прыжка можно набрать только 1 или 2, а после второго — только 4 или 5.
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|
| 2 | |
|
Разбор
Динамическое программирование, биномиальные коэффициенты.
Смотри рисунок.
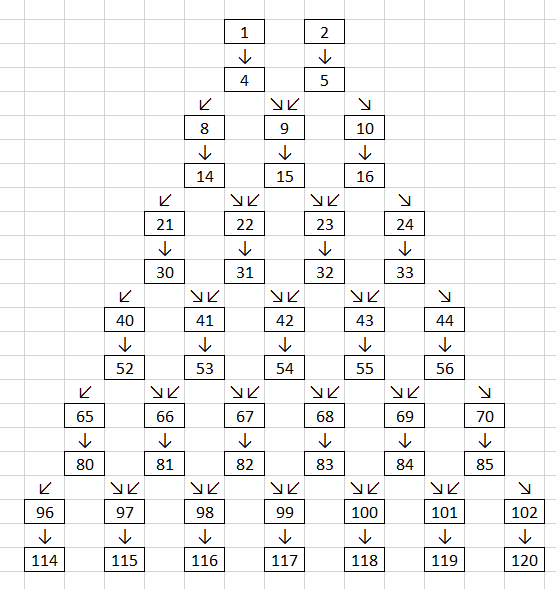
Попробуем определить по номеру пружка jump левую границу диапазона суммы, которую можно набрать за это количество прыжков. У нас будет jump1 = jump/2 (с округлением вверх) прыжков на одной ноге и jump2 = jump/2 (с округлением вниз) прыжков на двух ногах.
Левая граница, очевидно будет получаться при выборе наименьших чисел, то есть она равна сумме членов арифметической прогрессии 1, 4, 7, 10, ..., где количество слагаемых равно jump1 и сумме членов арифметической прогрессии 3, 6, 9, 12, ..., где количество слагаемых равно jump2. Правая граница будет равна левой границе, увеличенной на jump1.
Будем увеличивать jump (от начального значения 1) на 1, пока правая граница меньше n.
Если для найденного jump не выполняется условие Левая граница ≤ n ≤ Правая граница, то ответ равен нулю, в противном случае он равен биномиальному коэффициенту для строки с номером jump и позицией n - Левая граница + 1. Вычислить его можно с помощью динамического программирования или рекурсивно (но так можно не уложиться в TL).