Задача G. Жизнь чисел на дереве ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 256 Мб | |
| Выходной файл: | Стандартный выход |
Условие
Все натуральные числа разместились в узлах бинарного дерева по порядку (сверху вниз, слева направо). На рисунке Вы можете видеть верхнюю часть дерева.
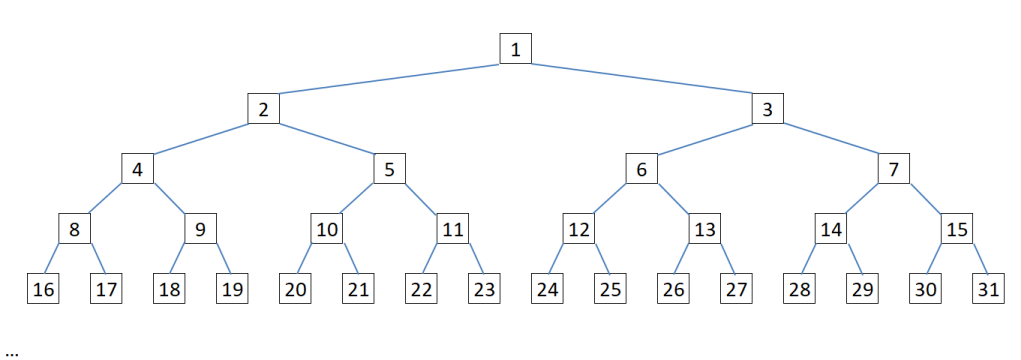
Возможно ли, двигаясь от корня по рёбрам, набрать в сумме число n?
Формат входных данных
Единственная строка входных данных содержит натуральное число n.
Обратите внимание, что при заданных ограничениях для хранения ответа необходимо использовать 64-битный тип данных, например long long в C++, int64 в Free Pascal, long в Java.
Формат выходных данных
Выведите в первой строке Yes или No — ответ на вопрос задачи.
Если нужную сумму набрать возможно, выведите во второй строке через пробел в порядке возрастания последовательность натуральных чисел — искомый маршрут.
Ограничения
1 ≤ n ≤ 1018
Пояснение к примеру
В первом примере сумму n = 5 набрать невозможно.
Во втором примере сумму n = 16 набрать можно, если сложить числа 1, 2, 4 и 9.
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|
| 2 | |
|
Разбор
Бинарный поиск.
Поскольку каждый узел k порождает узлы 2k и 2k+1, путь от некоторого узла a до корня будет представлять собой последовательность a, a/2, a/4, a/8, ..., 1, где знак / означает целочисленное деление с округлением вниз. Это значит, что для любого узла мы сможем быстро (за логарифм) посчитать сумму чисел от него до корня.
При этом для любых различных a < b:
a < b, a / 2 ≤ b / 2, a / 4 ≤ b / 4, и так далее. На рисунке рядом с каждым натуральным числом на дереве подсчитана набранная сумма.
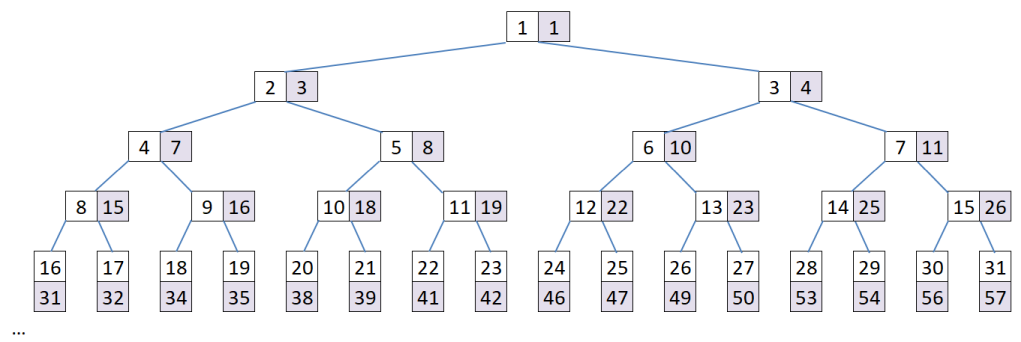
Тогда, поскольку у большего натурального числа получающаяся сумма больше, чем для любого меньшего, возможно применить бинарный поиск и найти наименьшее число, для которого набранная сумма не меньше n.