Задача C. Шагающий циркуль ≡
| Автор: | Г. Гренкин | Ограничение времени: | 2 сек | |
| Входной файл: | input.txt | Ограничение памяти: | 64 Мб | |
| Выходной файл: | output.txt |
Условие
Первоклассник нарисовал на бумаге две различные точки: A и B. Он воткнул ножку шагающего циркуля в точку A, другая ножка не касалась бумаги. Если он теперь воткнёт вторую ножку в произвольную точку плоскости, до которой дотягивается циркуль, а затем вытащит из бумаги первую ножку, то такое действие будет называться шагом циркуля.
Найти наименьшее количество шагов циркуля, которое нужно сделать, чтобы одна из его ножек оказалась в точке B. Раствор циркуля (т. е. длина шага) s может изменяться от s1 до s2 включительно (s1 ≤ s ≤ s2).
Формат входного файла
Первая строка содержит вещественные числа xA yA xB yB — координаты точек A и B.
Вторая строка содержит вещественные числа s1 s2.
Формат выходного файла
Выходной файл должен содержать единственное целое число — минимальное количество шагов циркуля.
Ограничения
− 70 < xA, yA, xB, yB < 70,
1 ≤ s1 ≤ s2 < 100.
Все входные данные имеют не более двух знаков после запятой и заданы точно (не содержат ошибки округления).
Примеры тестов
| № | Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|---|---|
| 1 | |
|
Разбор
Воспользуемся методом обратной задачи: по количеству шагов циркуля будем искать множество точек, до которых можно дойти за данное количество шагов.
Обозначим через Di множество точек, до которых от точки A можно дойти за i шагов.
Множество D0 состоит из одной единственной точки A.
D1 — множество точек M таких, что s1 ≤ AM ≤ s2. Это кольцо с центром в точке A.
Что значит, что точка M принадлежит множеству D2? Это значит, что существует точка N∈D1 такая, что s1 ≤ NM ≤ s2, т.е. до точки N можно дойти из точки A за один шаг и из точки N можно шагнуть в точку M.
Геометрически D2 — это объединение колец с центрами в точках множества D1 и радиусами s1 и s2. Объединение всех этих колец образует круг с центром в точке A радиуса 2s2.
Аналогично строятся множества D3, D4 и так далее. Множество Di(i > 1) — это круг с центром в точке A радиуса i × s2.
Определим множество с наименьшим номером, содержащее точку B.
Если  , то ответ — 1 шаг.
Если
, то ответ — 1 шаг.
Если 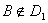 , то нужно решить неравенство
, то нужно решить неравенство 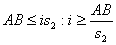 ,
поэтому ответ —
,
поэтому ответ — 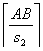 — наименьшее целое число, которое больше либо равно
— наименьшее целое число, которое больше либо равно
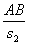 , или частное
, или частное 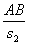 , округлённое вверх.
, округлённое вверх.
В случае, когда точка B лежит внутри круга с центром в A радиуса s1, решив неравенство, мы получим 1 вместо 2, поэтому этот случай нужно рассмотреть отдельно.
Замечание. Траекторию движения циркуля можно легко построить с помощью циркуля и линейки.