Задача B. Стиральный вопрос ≡
| Автор: | Г. Гренкин | Ограничение времени: | 2 сек | |
| Входной файл: | input.txt | Ограничение памяти: | 64 Мб | |
| Выходной файл: | output.txt |
Условие
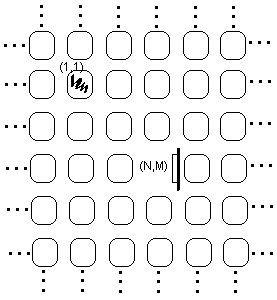
На склад завезли большую партию стиральных машин и расставили их так, как показано на рисунке. Когда машины уже были расставлены, на одной из них была обнаружена вмятина. Теперь рабочие должны переместить помятую машину к выходу.
Рабочие могут передвигать стиральную машину на свободное место, соседнее с ней по горизонтали или вертикали.
Требуется определить минимальное количество перемещений стиральных машин, которое придётся сделать рабочим.
В начальный момент времени координаты помятой машины — (1, 1), координаты выхода — (N, M), свободное место расположено в тех же координатах, что и выход.
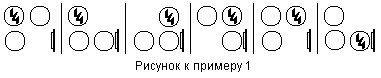
Формат входного файла
Входной файл содержит два целых числа N M.Формат выходного файла
Выходной файл должен содержать единственное целое число — минимальное количество перемещений.Ограничения
2 ≤ N, M ≤ 106Примеры тестов
| № | Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|---|---|
| 1 | |
|
| 2 | |
|
| 3 | |
|
Разбор
Перемещения стиральных машин следует начать с пододвигания свободного места к помятой машине. После пододвигания мы имеем два случая: либо свободное место находится справа от помятой машины, либо снизу.
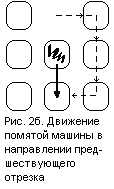
Для удобства решения задачи сведём второй случай к первому, применив к рисунку
поворот и осевую симметрию (см. рис. 1). 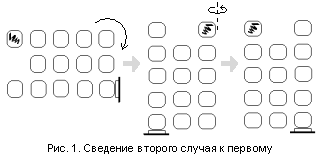
Для пододвигания свободного места нужно будет сделать (минимальное количество) (N + M − 3) перемещений. Докажем это. Рассмотрим функцию φ(x, y) = |x − x0| + |y − y0|, где (x, y) — текущие координаты свободного места, (x0, y0) — координаты свободного места после пододвигания: (x0, y0) = (2, 1) или (x0, y0) = (1, 2). Изначально φ(x, y) = φ(N, M) = N + M − 3, после пододвигания φ(x, y) = φ(x0, y0) = 0. Заметим, что за одно перемещение φ(x, y) может уменьшиться не более, чем на 1. Следовательно, пододвигание потребует не менее φ(N, M) − φ(x0, y0) = N − M + 3 перемещений стиральных машин.
Итак, мы свели исходную задачу к новой: найти минимальное количество перемещений стиральных машин, которое нужно сделать, чтобы передвинуть помятую стиральную машину к выходу, если изначально помятая машина имеет координаты (1, 1), свободное место — (2, 1), место возле выхода — (n, m). Обозначим ответ новой задачи f(n, m). Тогда ответ исходной задачи (N + M − 3) + min{f(N, M), f(M, N)}.
Решим новую задачу. Рассмотрим ряд случаев: каждый случай — это траектория движения
помятой машины. Решим задачу для каждого случая в отдельности.
Наименьший ответ, полученный для этих случаев, будет ответом в новой задаче.
Рассмотрим отдельный случай. Пусть помятая машина движется по определённой траектории. Требуется найти минимальное количество перемещений стиральных машин, которое для этого нужно. Количество перемещений для движения по данной траектории равно сумме количеств перемещений для движения по отдельным единичным отрезкам этой траектории. Нужно минимизировать эту сумму. Слагаемые этой суммы не зависят друг от друга, поэтому для нахождения минимального значения суммы найдём минимальные значения слагаемых, а полученные результаты сложим. Итак, минимальное количество перемещений для движения по траектории равно сумме минимальных количеств перемещений для движения по отдельным отрезкам этой траектории.
Чему равно минимальное количество перемещений стиральных машин для движения помятой
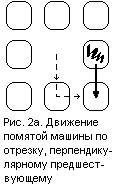
машины по некоторому отрезку её траектории? Рассмотрим два случая (см. рис. 2а, 2б).
Положение свободного места до движения по отрезку определяется направлением
движения по предшествующему отрезку. В случае а) потребуется 3 перемещения, в случае б) —
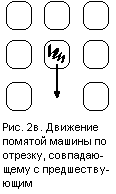
5 перемещений. Случай в) мы не рассматриваем, так как в этом случае помятая машина
делает лишние передвижения, двигаясь туда-сюда.
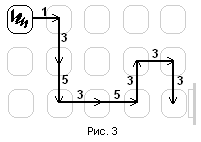
Таким образом, имеем правило для нахождения минимального количества перемещений стиральных машин для движения помятой машины по данной траектории (см. рис. 3): если при движении по отрезку траектории помятая машина изменила направление движения, то этому отрезку следует приписать число 3, в противном случае — число 5. Первому отрезку траектории следует приписать число 1. Затем все эти числа нужно сложить — это и будет минимальное количество перемещений.
Теперь найдём траекторию, для которой вычисленное по правилу значение будет минимальным.
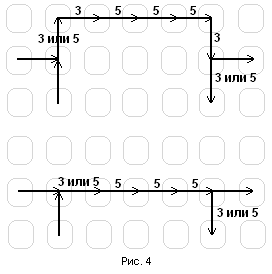 Сначала найдём длину искомой траектории. Для этого покажем, что траектория должна идти только
вправо или вниз. Рассмотрим часть траектории, изображённую на рисунке 4а: помятая
машина при своём движении поднялась на одну единицу вверх, затем прошла k единиц вправо,
после чего спустилась вниз на одну единицу.
Попробуем срезать путь по прямой (см. рис. 4б). Уменьшится ли сумма чисел,
приписанных отрезкам траектории?
Числа на неподписанных отрезках траектории и на отрезках, не попавших в рассматриваемую её часть,
не изменятся, поэтому их можно не рассматривать.
Сначала найдём длину искомой траектории. Для этого покажем, что траектория должна идти только
вправо или вниз. Рассмотрим часть траектории, изображённую на рисунке 4а: помятая
машина при своём движении поднялась на одну единицу вверх, затем прошла k единиц вправо,
после чего спустилась вниз на одну единицу.
Попробуем срезать путь по прямой (см. рис. 4б). Уменьшится ли сумма чисел,
приписанных отрезкам траектории?
Числа на неподписанных отрезках траектории и на отрезках, не попавших в рассматриваемую её часть,
не изменятся, поэтому их можно не рассматривать.
Сумма чисел в случае а) равна
(3 или 5) + 3 + 5(k − 1) + 3 + (3 или 5) ≥ 3 + 3 + 5(k − 1) + 3 + 3 = 5(k − 1) + 2.
Сумма чисел в случае б) равна
(3 или 5) + 5(k − 1) + (3 или 5) ≤ 5 + 5(k − 1) + 5 = 5(k − 1).
Таким образом, при срезании пути сумма чисел, которая есть минимальное количество перемещений
стиральных машин для движения помятой машины по данной траектории, всегда уменьшается.
 К траектории помятой машины, которая поднимается вверх более, чем на одну единицу,
можно применить последовательное срезание самых верхних подъёмов (см. рис. 5).
Случай движения помятой машины влево рассматривается аналогично.
К траектории помятой машины, которая поднимается вверх более, чем на одну единицу,
можно применить последовательное срезание самых верхних подъёмов (см. рис. 5).
Случай движения помятой машины влево рассматривается аналогично.
Итак, искомая оптимальная траектория идёт только вправо или вниз.
По доказанному выше её длина l равна n + m − 2.
l = 1 + c + s,
где c — число отрезков, перпендикулярных предшествующим, s — число отрезков,
идущих в направлении предшествующих.
Минимальное количество перемещений для данной траектории равно
x = 1 + 3c + 5s = 1 + 5(c + s) − 2c = 5l − 4 − 2c.
Чтобы найти минимальное значение x, нужно найти максимальное значение c,
так как первые два слагаемых постоянны.
Пусть h — число горизонтальных отрезков траектории,
v — число вертикальных отрезков траектории,
ch — число горизонтальных отрезков траектории, следующих за вертикальными,
cv — число вертикальных отрезков траектории, следующих за горизонтальными.
l = h + v, c = ch + cv;
ch ≤ h − 1, cv ≤ v;
ch ≤ v, cv ≤ h;
ch ≤ min{h − 1, v}, cv ≤ min{h, v};
h ≤ n − 1, v ≤ m − 1.
Следовательно, c = ch + cv ≤ min{n − 2, m − 1} + min{n − 1, m − 1}.
Полученная оценка сверху для c достижима для любых n и m (см. рис. 6).
Следовательно, f(n, m) = min x = 5l − 4 − 2(min{n − 2, m − 1} + min{n − 1, m − 1}) = 5(n + m − 2) − 4 − 2(min{n − 1, m} − 1 + min{n, m} − 1) = 5n + 5m − 2(min{n − 1, m} + min{n, m}) − 10.
Ответ: (N + M − 3) + min{f(N, M), f(M, N)}.