Задача B. Расстановка часовых ≡
| Автор: | Антон Карабанов, математический фольклор | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 64 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
Широко известна следующая математическая задача для младших школьников:
Вдоль стен квадратного бастиона требовалось поставить 16 часовых. Комендант разместил их так, как показано на рисунке слева, по 5 человек с каждой стороны.
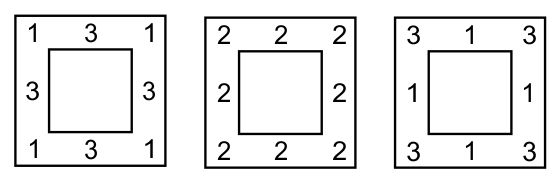
Затем пришёл полковник и, недовольный размещением часовых, распорядился поставить солдат так, чтобы с каждой стороны их было по 6. Вслед за полковником пришёл генерал, рассердился на полковника за его распоряжение и разместил солдат по 7 человек с каждой стороны. Каково было размещение в двух последних случаях? Ответы на этот вопросы на рисунке по центру и справа.
Попробуйте решить обобщенную задачу: вдоль стен квадратного бастиона требовалось поставить n часовых, по k человек с каждой стороны. При этом количество часовых на всех углах бастиона должно быть одинаковым и количество часовых на всех его стенах тоже должно быть одинаковым. Удастся ли это сделать и каким образом?
Формат входных данных
Две строки входного файла содержат два натуральных числа: n и k.
Формат выходных данных
Выведите через пробел два неотрицательных целых числа — количество часовых на любом из углов и на любой из стен. Выведите -1, если часовых расставить нельзя.
Ограничения
1 ≤ k, n ≤ 109
Система оценки и описание подзадач
Баллы за каждый тест начисляются независимо.
Пояснения к примерам
Первый пример соответствует случаю из условия.
Во втором примере часовых расставить требуемым образом невозможно.
В третьем примере требуемая расстановка приведена на рисунке ниже.
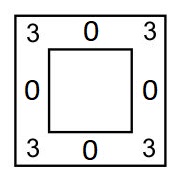
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|
| 2 | |
|
| 3 | |
|