Problem C. Covering the ring ≡
| Author: | A. Baranov | Time limit: | 1 sec | |
| Input file: | input.txt | Memory limit: | 256 Mb | |
| Output file: | output.txt |
Statement
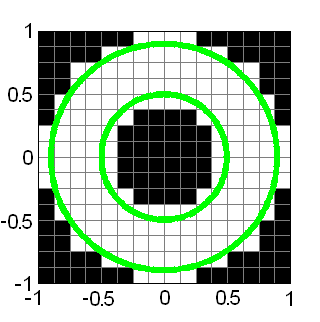
Let us consider a rectangular domain D = {(x, y): Ax ≤ x ≤ Bx, Ay ≤ y ≤ By} covered by the uniform grid (two-dimensional array of cells):
Ωi j = {(x, y): xi < x < xi + 1, yj < y < yj + 1}, where xi = Ax + (i − 1) ⋅ Sx, yj = Ay + (j − 1) ⋅ Sy, i = 1, 2, …, Nx, j = 1, 2, …, Ny,
Sx = (Bx − Ax) / Nx, Sy = (By − Ay) / Ny — grid steps for x and y respectively.
The grid is defined by four real parameters (Ax, Ay, Sx, Sy) and two integer parameters (Nx, Ny).
Note that cells are open rectangles not including their boundaries.
Your program must count grid cells that have common points with the ring defined by its center (x0, y0), internal and external radius (r1, r2).
Input file format
Input file contains parameters of the grid: Ax, Ay, Sx, Sy, Nx, Ny, followed by parameters of the ring: x0, y0, r1, r2.
Output file format
Output file must contain a single integer — number of cells intersecting the ring.
Constraints
All input values have no more than 5 digits after the decimal point.
− 10 < (Ax, Ay) < 10, 1 ≤ (Bx − Ax) < 10, 1 ≤ (By − Ay) < 10, 0 < (Nx, Ny) ≤ 106,
− 10 < (x0, y0) < 10, 0 ≤ r1 ≤ r2 < 10
Sample tests
| No. | Input file (input.txt) |
Output file (output.txt) |
|---|---|---|
| 1 | |
|
| 2 | |
|