Задача 6B. Съемка заповедника ≡
| Автор: | ONTI | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 256 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 15 |
Условие
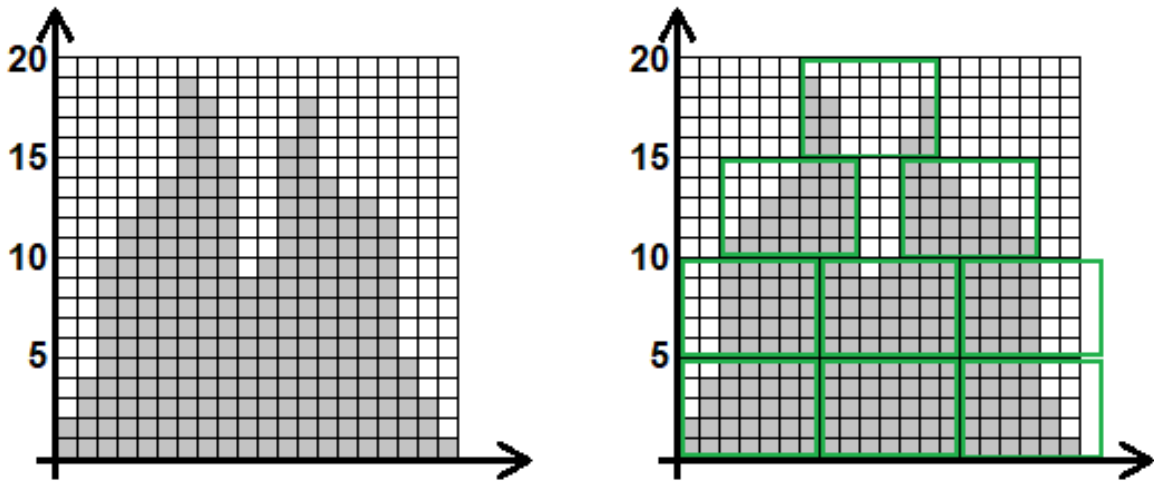
Администрация некоторого заповедника хочет заказать спутниковые снимки на всю его площадь. Территория заповедника имеет форму криволинейной трапеции, которую мы для простоты будем представлять как набор прямоугольников ширины 1 и различной высоты. Для лучшего понимания посмотрите на чертеж.
Каждый снимок имеет вид прямоугольника с шириной a и высотой b. Стороны прямоугольника должны быть параллельны осям координат. Поворачивать снимки нельзя. Снимки могут выходить за границу заповедника или накладываться друг на друга. При заказе каждого снимка можно указать его местоположение. Администрация заповедника хочет заказать как можно меньше снимков.
Напишите программу, которая позволит расположить минимальное количество снимков заданного размера на плоскости так, чтобы они покрыли всю территорию заповедника. В качестве ответа ваша программа должна вывести количество снимков.
Формат входных данных
На вход программы в первой строке через пробел подаются три натуральных числа n, a, b — ширина криволинейной трапеции (количество столбиков из которых состоит трапеция), а также ширина снимка и высота снимка. 1 ≤ n ≤ 2000; 1 ≤ a ≤ 2000; 1 ≤ b ≤ 5000. Во второй строке через пробел записаны n целых неотрицательных чисел h1... hn — высоты столбиков. 0 ≤ hi ≤ 5000.
Формат выходных данных
Требуется вывести одно число — минимальное количество снимков.
Методика проверки и пояснение к тесту Рисунки в условии задачи соответствуют тесту. Как видно из рисунков, минимальное количество снимков равно девяти.
Программа проверяется на 15 тестах. Прохождение каждого теста оценивается в 1 балл. Тест из условия задачи при проверке не используется.
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|
Разбор
При построении стратегии покрытия территории заведника прямоугольниками можно использовать жадный алгоритм. Каждый из прямоугольников можно располагать так, чтобы его левый нижний угол попадал на самый левый из непокрытых квадратиков. В этом случае снимки будут располагаться, как показано на рисунке, по слоям.
В предлагаемом решении для упрощения высота каждого столбика делится на высоту снимка с округлением вверх. Такое преобразование позволяет далее предполагать, что все снимки имеют высоту равную единице. После этого основное решение записыватся в два цикла. Внешний цикл пробегает по высоте столбиков. Вложенный цикл ищет самый левый квадратик, принадлежащий заповеднику. В случае успеха счетчик в цикле увеличивается на ширину снимка, а количество снимков увеличивается на единицу.