Задача C. Охота на шушанчиков ≡
| Автор: | А. Жуплев, А. Кленин | Ограничение времени: | 2 сек | |
| Входной файл: | input.txt | Ограничение памяти: | 64 Мб | |
| Выходной файл: | output.txt | |||
| Максимальный балл: | 100 |
Условие
|
Чтобы наловить шушанчиков, Крокодил Гена отправляется в лес с чемоданом и ружьём, стреляющим усыпляющими дротиками. В лесу он становится в точку с координатами (XG; YG) и начинает внимательно смотреть по сторонам. Как только Гена видит шушанчика, он тут же стреляет в него, и скоро спящий шушанчик оказывается в чемодане Крокодила. Гена всегда стреляет мгновенно и точно. Лес состоит из N деревьев. На плане i-ое дерево можно представить в виде круга с координатами центра (Xi; Yi) и радиусом Ri. Гена видит все точки с координатами (x, y), такие, что отрезок (x; y) − (XG; YG) не пересекает ни одно дерево. Один шушанчик, гуляя по лесу, пришёл в точку с координатами (XS; YS). Услышав, что Крокодил Гена в лесу, он бросился бежать в нору с координатами (XH; YH). Требуется определить, сможет ли шушанчик добраться до норы так, чтобы Гена его не увидел. |

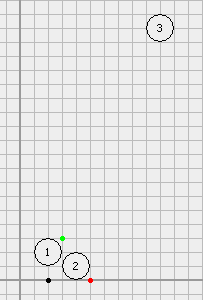
|
Формат входного файла
Входной файл состоит из K тестов. В первой строке входного файла содержится число K. Далее следуют описания тестов.
Каждый тест описывается числами XS YS XH YH XG YG N, за которыми следуют N троек чисел Xi Yi Ri.
Формат выходного файла
В выходном файле должно содержаться K строк, каждая из которых должна равняться ESCAPE, если шушанчик из соответствующего теста сможет добраться до норы, или CATCH, если не сможет.
Ограничения
1 ≤ K ≤ 10
− 100 ≤ XS, YS, XH, YH, XG, YG, Xi, Yi ≤ 100
1 ≤ Ri ≤ 100, 0 ≤ N ≤ 100
Деревья не пересекаются и не касаются. Позиции Гены, шушанчика и норы различаются и не находятся внутри деревьев.
Все числа во входном файле целые
Примеры тестов
| № | Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|---|---|
| 1 | |
|
Разбор
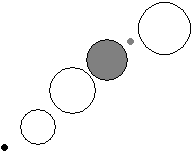 Сведём исходную задачу к задаче о существовании пути между двумя вершинами (u и v) в графе.
Вершинам графа будут соответствовать деревья. Смежность вершин i и j будет означать,
что шушанчик может перемещаться вне поля зрения Крокодила между деревьями i и j.
Вершинам u и v соответствуют деревья за которыми находятся шушанчик и нора.
Сведём исходную задачу к задаче о существовании пути между двумя вершинами (u и v) в графе.
Вершинам графа будут соответствовать деревья. Смежность вершин i и j будет означать,
что шушанчик может перемещаться вне поля зрения Крокодила между деревьями i и j.
Вершинам u и v соответствуют деревья за которыми находятся шушанчик и нора.
Дерево, за которым находится точка p — это дерево, находящееся как можно дальше от Крокодила, но ближе к нему, чем точка p.
Возможный алгоритм реализации: среди всех окружностей, пересекающихся с отрезком SQ (Q — точка, для которой требуется определить дерево, за которым она находится) нужно выбрать такую окружность, что длина отрезка SP максимальна (P - наиболее удалённая от S точка пересечения SQ с окружностью). Если SQ не пересекает ни одной окружности — это означает, что точка Q не находится ни за одним деревом (в этом случае ответом будет CATCH).
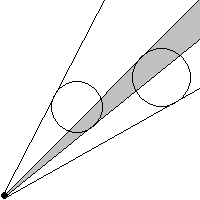
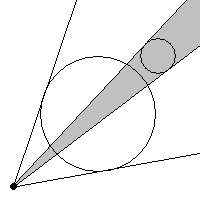
Рассмотрим все пары окружностей. Возможны три ситуации взаимного расположения этих пар и точки S:
- Углы, под которыми окружности видны из точки S не пересекаются. В этом случае соответствующие вершины не смежны.
- Углы, под которыми окружности видны из точки S пересекаются, но существуют точки углов, которые не принадлежат их пересечению. В этом случае между соответствующие вершины смежны.
- Один из углов, под которыми окружности видны из точки S, находится в другом. В этом случае вершины будут смежными тогда и только тогда, когда окружность, которая видна под меньшим углом, ("внутренняя") будет находится по отношению к точке S за окружностью, видной под большим углом ("внешняя").
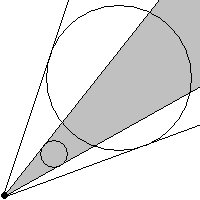
Возможный алгоритм реализации: Угол, под которым окружность видна из данной точки — угол между касательными к данной окружности, выходящими из точки, поэтому для задания угла видимости достаточно знать полярный угол обоих касательных. Обозначим полярные углы касательных α1, α2 и β1, β2 к одной и второй окружностям соответственно. Для удобства будем считать, что α1 < α2, β1 < β2. Рассмотрим все три ситуации в этих обозначениях (с точностью до перестановки α и β местами):
- α2 < β1.
- α1 < β1 < α2 < β2.
- α1 < β1 < β2 < α2. Пусть R — точка касания касательной к "внутренней" окружности, а точка T — точка пересечения этой касательной с "внешней". Условие SR > ST означает, что "внутренняя" окружность находится за "внешней" по отношению к S.
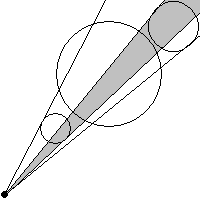
Оказывается, что изложенные условия существования ребра между двумя вершинами, являются необходимыми, но не достаточными (последний рисунок это демонстрирует). Поэтому будем рассматривать лишь те пары окружностей, между которыми нет никаких других.
Теперь, когда матрица смежности графа построена, для нахождения пути можно запустить, например, поиск в глубину.
 |
 |
 |
 |
 |
| α2 < β1 | α1 < β1 < α2 < β2 | α1 < β1 < β2 < α2 и SR < ST | α1 < β1 < β2 < α2 и SR > ST | Существует окружность между двумя рассматриваемыми |