Задача A. Табун ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 256 Мб | |
| Выходной файл: | Стандартный выход |
Условие
Однажды черный шахматный король, живущий на доске размером n × m, решил собрать большой табун белоснежных коней. Король для себя и коней может выбрать любые поля на доске. Конечно, ни один белый конь не должен атаковать черного короля. Какое минимальное количество пустых полей окажется на доске?
Формат входных данных
Единственная строка входного файла содержит два натуральных числа, записанных через пробел: n и m — размер шахматной доски.
Формат выходных данных
Выведите одно неотрицательное целое число — ответ на вопрос задачи.
Ограничения
1 ≤ n, m ≤ 10
Система оценки и описание подзадач
Баллы за каждый тест начисляются независимо.
Пояснение к примеру
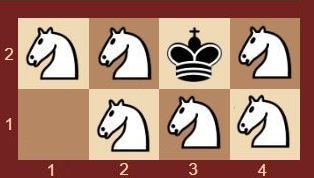
В примере на доске размером 2 × 4 какое бы место для себя не выбрал король, более 6 коней разместить нельзя. Одно поле останется пустым.
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|
Разбор
Разбор случаев. Пусть n — меньшая из двух сторон.
1. Ответ будет равен нулю, если:
a) n = 1 (узкая доска шириной в одну клетку);
b) n = 2 и m меньше 4 (доска 2 на 2 или 2 на 3);
с) n = 3 и m = 3 (квадратная доска, король в центре);
2. Ответ будет равен единице, если n = 2 и m больше 3 (смотри пример, король в углу);
3. Ответ будет равен двум для всех остальных досок, король стоит в углу.