Задача C. Снежки ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 256 Мб | |
| Выходной файл: | Стандартный выход |
Условие
Прежде чем играть в снежки с соседскими ребятами, Тимофею их нужно заранее слепить и удобно сложить. Ведь соперников много, а он один, поэтому времени на подготовку уходит много.
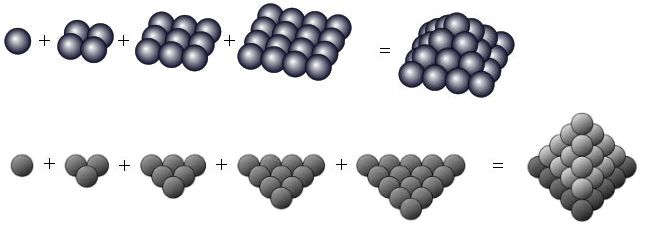
Первую кучку мальчик складывает так: нижний слой снежков в форме квадрата со стороной k, на него — слой снарядов со стороной k − 1, и так далее. На самом верху лежит один снежок.
Вторую кучку он складывает так: нижний слой снежков в форме правильного треугольника со стороной t, на него — слой снарядов со стороной t − 1, и так далее. На самом верху, опять-таки лежит один снежок.
На рисунке ниже Вы можете видеть первую кучку высотой 4 слоя (в ней 16 + 9 + 4 + 1 = 30 снежков) и вторую кучку высотой 5 слоёв (в ней 15 + 10 + 6 + 3 + 1 = 35 снежков).
Помогите Тимофею определить, возможно ли ровно n снежков разложить на две такие кучки? Разумеется, в каждой из кучек должно быть хотя бы по одному снежку.
Формат входных данных
Единственная строка входного файла содержит натуральное число n — количество снежков у Тимофея.
Формат выходных данных
Выведите Yes или No — ответ на вопрос задачи.
Ограничения
1 ≤ n ≤ 1015
Пояснения к примерам
В первом примере дано n = 3. Разложить на две кучки невозможно.
Второй пример разобран в условии задачи.
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|
| 2 | |
|
Разбор
Два указателя.
Сформируем два массива (соответствующие количеству снежков в пирамидках первого и второго типов), отсортируем их и проверим, равно ли число n сумме каких-нибудь двух чисел из этих массивов.