Задача B. Дважды два ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 256 Мб | |
| Выходной файл: | Стандартный выход |
Условие
На одном из Тихоокеанских островов принято решение о внесении ровно одного изменения в таблицу умножения. Согласно новому порядку, теперь при умножении цифры a на цифру b (и наоборот) получается ровно n. По предложенному произведению двух многозначных чисел определите эти цифры и их новый результат умножения.
Считайте, что 1 ≤ a, b ≤ 9 и 0 ≤ n ≤ 99.
Формат входных данных
Три строки входного файла содержат два натуральных и одно целое неотрицательное числа: x, y и p. Первые два числа — множители, третье — их произведение, вычисленное по новым правилам. Гарантируется, что x × y ≠ p при обычном вычислении.
Формат выходных данных
Выведите в трёх строках в том же формате три натуральных числа a, b и n — изменение в таблице умножения. Гарантируется, что во всех тестах такое изменение единственно (в общем случае это не так). Числа a и b выведите в порядке не убывания.
Ограничения
10 ≤ x, y ≤ 109
0 ≤ p ≤ 1018
Пояснение к примеру
В примере в таблицу умножения было внесено изменение 3 × 4 = 15. Смотри рисунок: слева умножение по обычным правилам, справа — по новым. Красным цветом выделены изменившиеся цифры.
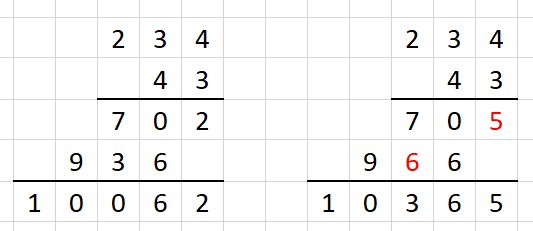
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|
Разбор
Полный перебор.
Тремя вложенными циклами (по a, b, и n) переберем все возможные изменения в таблице умножения.
Осталось реализовать функцию, которая реализует умножение двух натуральных чисел по новым правилам (через умножение однозначного числа на многозначное и накопление суммы, совершенно аналогично тому, как мы это делаем вручную "в столбик").