Задача B. Разрезание многогранника ≡
| Автор: | А. Баранов | Ограничение времени: | 1 сек | |
| Входной файл: | input.txt | Ограничение памяти: | 512 Мб | |
| Выходной файл: | output.txt | |||
| Максимальный балл: | 100 |
Условие
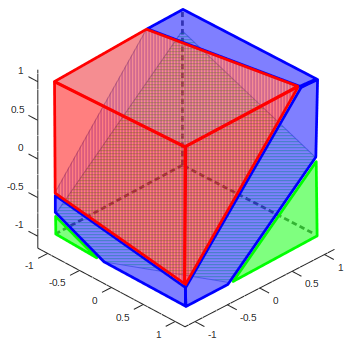
Пусть имеется выпуклый многогранник и две плоскости, каждая из которых задается ортогональным к ней вектором U⃗k.
Известно, что плоскость можно сдвигать относительно начала координат
путем смещения всех составляющих ее точек на вектор S⃗k = tk ⋅ U⃗k|U⃗k|, где tk — произвольный скалярный параметр.
Требуется расположить указанные плоскости таким образом,
чтобы они разбивали исходный многогранник ровно на три части одинакового объема.
Формат входного файла
В начале входного файла "input.txt" записано число N, за которым следует 3 × N вещественных координат вершин.
Далее указано число M, за которым следует M граней, записанных в следующем виде.
Вначале для каждой грани указано число ее вершин, за которым следуют их индексы,
перечисленные в порядке их обхода для получения ограничивающего цикла грани.
При этом полагается, что нумерация вершин начинается с нуля.
В окончании входного файла записаны компоненты векторов, задающих плоскости
(сначала для 1-го, а затем для 2-го).
Формат выходного файла
Если решение существует, в выходной файл "output.txt" следует вывести число 1
и пару вещественных параметров t1 и t2, указанных с точностью не менее 5-го знака после запятой.
В противном случае, выходной файл должен содержать единственное число 0.
Ограничения
Исходный многогранник является невырожденным (имеет ненулевой объем).
Все грани представляют собой выпуклые многоугольники.
Координаты всех вершин по модулю не превосходят 10.
Число вершин и граней не превосходит 100.
Гарантируется, что в пределах заданной
точности ответ может быть
получен однозначно.
Примеры тестов
| № | Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|---|---|
| 1 | |
|
Разбор
Обрезка выпуклого многогранника
Для начала разберемся с алгоритмом, выполняющим обрезку выпуклого многогранника с выпуклыми гранями заданной плоскостью.
Разделим вершины исходного многогранника относительно секущей плоскости:
- внутренние — вершины, лежащие в заданной плоскости (с учетом погрешности округления);
- верхние — вершины, лежащие выше заданной плоскости;
- нижние — вершины, лежащие ниже заданной плоскости.
Для этого достаточно будет проверить знак скалярного произведения (X⃗i − C⃗) ⋅ U⃗,
где X⃗i — координаты текущей вершины;
C⃗ — произвольная точка плоскости (с учетом ее смещения);
U⃗ — нормаль к плоскости.
Все внутренние и верхние вершины добавляем в результирующий список P.
Далее из ребер многогранника выделим следующие разновидности:
- внутренние — у которых обе вершины являются внутренними;
- секущие — если одна вершина верхняя, а другая нижняя;
- верхние — если есть верхняя, но нет нижней вершины;
- нижние — если есть нижняя, но нет верхней вершины.
На каждом секущем ребре определим точку, в которой оно пересекает плоскость, и сформируем на ее основе новую вершину.
Само ребро при этом укорачиваем путем замены его нижней вершины на новую.
Отдельно для каждого ребра запоминаем список его вершин, лежащих в плоскости (включая новую).
Добавляем новую вершину в результирующий список вершин P. Все ребра, кроме нижних, добавляем в новый список E.
Далее рассмотрим двумерные грани и разделим их на:
- внутренние — у которых все ребра являются внутренними;
- секущие — есть секущее ребро, либо пара верхнее-нижнее;
- верхние — есть верхнее, но нет секущих/нижних ребер;
- нижние — есть нижнее, но нет секущих/верхних ребер.
Обратим внимание, что т.к. все грани выпуклые, то они не могут иметь секущее и внутреннее ребро одновременно.
Наличие внутреннего ребра также исключает существование пары из верхнего и нижнего ребер.
При этом секущая плоскость может проходить через последовательность внутренних ребер.
Можно также утверждать, что секущих ребер не может быть больше двух.
Руководствуясь этой логикой, пройдемся по ребрам секущей грани, собирая ранее приписанные к ним вершины.
Таких вершин всегда будет две. Сформируем из них новое ребро.
Саму грань при этом обрезаем, удалив из нее нижние ребра. Вместо них вставляем новое.
Для каждой грани запоминаем список ее ребер, лежащих в плоскости (включая новое).
Добавим новое ребро в результирующий список ребер E. Все грани, кроме нижних, добавляем в список F.
В завершение, если имелась секущая грань, либо пара верхняя-нижняя,
собираем лежащие в плоскости ребра и формируем новую грань.
В силу выпуклости, такая грань всегда будет одна.
Объем выпуклого многогранника
Чтобы посчитать объем полученного тела, достаточно будет разложить его на составляющие тетраэдры.
Для этого вычислим геометрический центр вершин многогранника, а также центры каждой из граней.
Далее, запустим обход ребер на каждой из граней.
Порядок обхода ребер здесь роли не играет.
Дополняя такое ребро центральной точкой грани
и центром многогранника,
получим тетраэдр, объем которого можно найти
по известной формуле.
Разбиение многогранника
Теперь рассмотрим способ разбиения многогранника объемом V0 на три равные части.
Выберем 1-ю плоскость, и разобьем наше тело на две части объемом 1 / 3 и 2 / 3 от V0 соответственно.
Будем искать соответствующий параметр t, отвечающий за смещение плоскости вдоль ее нормали.
Определим для него диапазон, на котором смещенная плоскость будет пересекать тело,
найдя минимум и максимум из проекций вершин на соответствующий вектор нормали.
В указанном диапазоне объем отсеченного тела будет монотонно расти от нуля до V0,
что дает нам возможность воспользоваться методом двоичного поиска.
После того, как нужное значение t было найдено, получим два тела: меньшее B1 и большее B2.
Задействуем вторую плоскость, и найдем интервал, на котором она пересекает B2.
Исключим из него подынтервал, на котором она пересекает тело B1.
Если этого не сделать, исходное тело может оказаться разбитым более чем на три части.
Запускаем аналогичный поиск, чтобы разбить тело B2 на две равные по объему части.
При этом, в отличие от первого разбиения, здесь поиск может завершиться неудачей,
если желаемый ответ окажется за пределами допустимого интервала.
Обратим внимание на то, что направление нормали 1-й плоскости определяет
часть тела, которую мы будем пытаться разбить 2-й плоскостью.
Поэтому в случае неудачи нормаль можно будет инвертировать
и попробовать еще раз.