Problem G. Gray, black and white squares ≡
| Author: | Антон Карабанов | Time limit: | 1 sec | |
| Input file: | Standard input | Memory limit: | 256 Mb | |
| Output file: | Standard output |
Statement
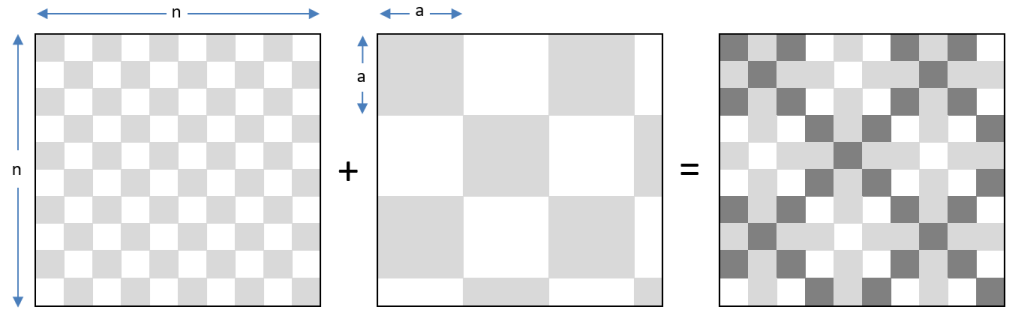
Timofey has two semi-transparent films with a gray-and-white checkered pattern, each of size n×n. The first film has a cell size of 1×1, and the second film has a cell size of a×a. Both films start with a gray square in the top-left corner.
Today, Timofey placed the two films on top of each other. As a result:
Where gray squares from both films overlapped, the color turned black.
Where gray squares overlapped with white squares, the color remained gray.
Where white squares overlapped with white squares, the color remained white.
Your task is to determine how many single-unit squares of black, gray, and white color there are in total.
Input format
The input consists of two natural numbers, a and n.
Output format
The output should be three natural numbers — the number of black, gray, and white unit squares.
Constraints
2≤a<n≤109
Example explanation
See the diagram for an example of tiling.
Sample tests
| No. | Standard input | Standard output |
|---|---|---|
| 1 | |
|