Задача A. Прогулка по сфере ≡
| Автор: | Dmitriy Merzlyakov | Ограничение времени: | 1 сек | |
| Входной файл: | input.txt | Ограничение памяти: | 512 Мб | |
| Выходной файл: | output.txt | |||
| Максимальный балл: | 100 |
Условие
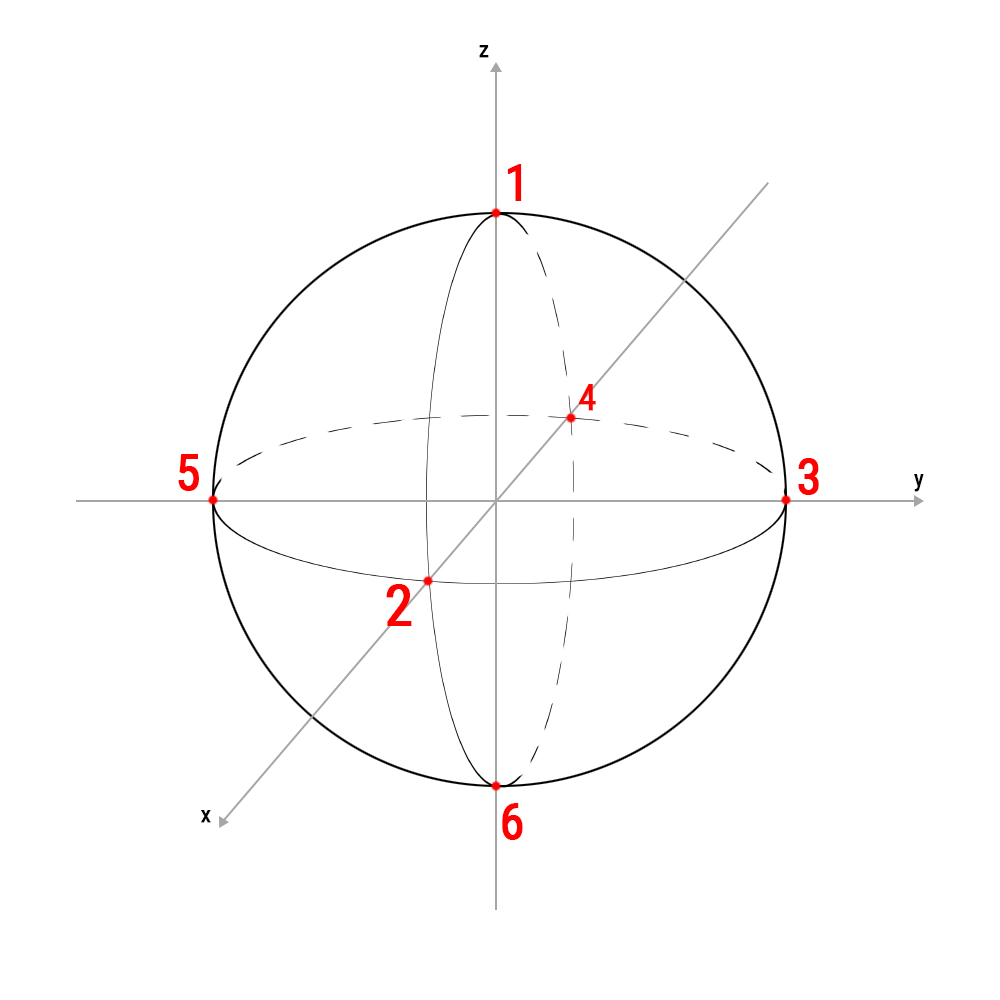
Некоторая планета Сигма имеет форму сферы. На Сигме есть только три дороги в виде больших окружностей в плоскостях OXY, OXZ и OYZ, пересечения которых пронумерованы так, как показано на рис. 1. Будем считать, что длина дороги между любыми двумя пересечениями равна 1, а сами точки пересечений назовём пунктами.
Юный программист Вася находится в пункте a и смотрит по направлению дороги, которая ведёт в пункт c. Он собирается совершить прогулку по этой планете до пункта b так, чтобы, оказавшись в нём, смотреть по направлению дороги к d. Однако не всё так просто: на планете действует запрет на совершение поворотов вокруг себя при движении.
Например, пусть вы находитесь в пункте 1 и смотрите вдоль дороги, которая ведёт в пункт 2. При движении в 2 вы будете идти прямо, затем, поскольку поворачиваться запрещено, из 2 в 3 вы сможете двигаться только левым боком, а возвращаясь из 3 в 1 вы будете перемещаться спиной вперёд. В результате этих действий вы снова окажетесь в пункте 1, однако теперь вы смотрите не на пункт 2, а на пункт 3 (см. рис. 2).
 |
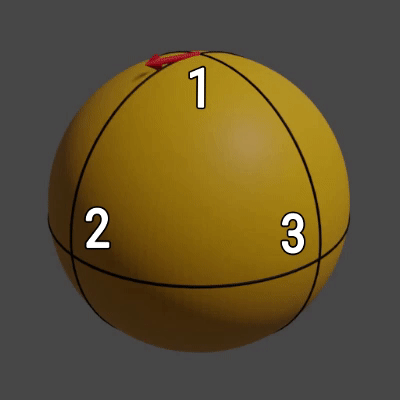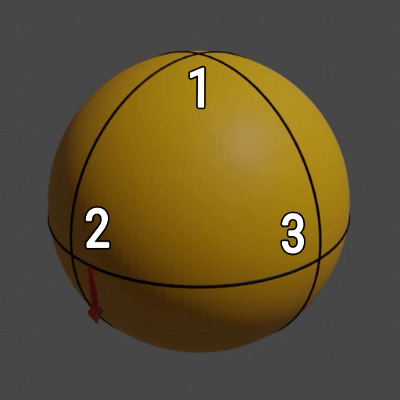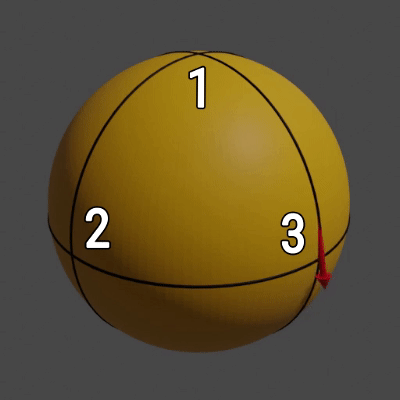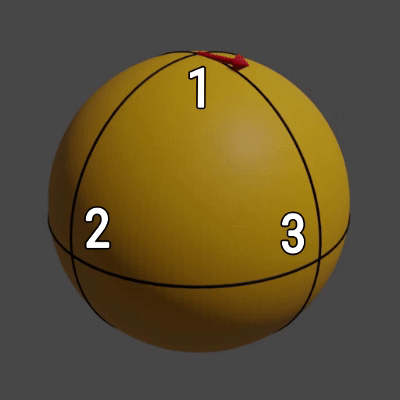 |
Заметив это, Вася понял, что если правильно построить маршрут, то он сможет добраться в b и развернуться в процессе прохождения пути так, чтобы при этом будучи в b смотреть по направлению в d. Вася не хочет затратить на это много времени и поэтому, чтобы оптимизировать свой путь, он хочет написать программу, которая по заданным параметрам a, b, c, d определила бы длину кратчайшего пути l из a в b при указанных условиях, а также выдавала бы последовательность пунктов, которые составляют этот путь. Помогите Васе написать такую программу.
Примечание
В качестве направлений c и d выбираются пункты, которые находятся от пунктов a и b соответственно на расстоянии 1. Например, находясь в пункте a = 1 можно смотреть в один из 4 пунктов c ∈ {2, 3, 4, 5}.
Гарантируется, что пара чисел (a, c) отличается от пары чисел (b, d), т.е. a ≠ b и c ≠ d одновременно.
Формат входного файла
В первой строке содержаться натуральные числа a и c, во второй строке находятся числа b и d.
Формат выходного файла
В первой строке требуется вывести одно число l – длину кратчайшего маршрута из a в b.
Во второй строке нужно вывести сам маршрут в виде последовательности чисел (через пробел) x1 x2... xl, где xi – номер i-го пункта в маршруте.
Если оптимальных маршрутов несколько, выведите любой из них.
Ограничения
1≤a, b, c, d≤6, a≠c, b≠d
Примеры тестов
| № | Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|---|---|
| 1 | |
|
| 2 | |
|