Задача G. Мосты-горки ≡
| Автор: | Г. Гренкин | Ограничение времени: | 2 сек | |
| Входной файл: | input.txt | Ограничение памяти: | 64 Мб | |
| Выходной файл: | output.txt |
Условие

Выбор подходящего проекта строительства моста на остров Русский — задача не из лёгких: ведь существует много разновидностей мостов.
В Академии был разработан новый тип мостов — мосты-горки. Эти мосты устанавливаются между двумя островами, один из которых должен быть высоким, а другой низким. Чтобы попасть с высокого острова на низкий, достаточно просто скатиться по мосту, как по горке. При этом даже не нужно тратить топливо! К тому же при достаточной массе автомобиля езда превращается в увлекательный аттракцион.
Но у мостов-горок есть и недостатки:
- Мост должен быть идеально прямым: массивные автомобили могут не справиться с поворотами на большой скорости.
- Конструкция мостов-горок такова, что один мост не может проходить над другим мостом, то есть мосты не должны пересекаться друг с другом.
Ввиду заинтересованности правительства в мостах-горках в Академии была организована лаборатория по их исследованию. В лабораторных условиях была создана модель архипелага, в котором N высоких и N низких островов представлены точками на плоскости, причём никакие три острова не лежат на одной прямой. Требуется построить ровно N мостов-горок между островами так, чтобы на каждом острове был мост. Как высокие, так и низкие острова пронумерованы от 1 до N.
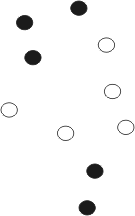
Первый пример теста соответствует рисунку справа. Тёмными изображены острова с номером 1, а светлыми — с номером 2. Если соединить тёмные острова со светлыми, то мосты будут пересекаться.
Формат входного файла
Входной содержит число N, за которым следует N пар чисел Xi Yi — координаты высоких островов, а затем N пар чисел xi yi — координаты низких островов.
Формат выходного файла
Выходной файл должен содержать N пар чисел pi qi — номера островов, соединённых мостом, где pi — номер высокого острова, qi — номер низкого острова. Пары можно выводить в произвольном порядке. Если решений несколько, выведите любое из них.
Если N мостов-горок построить невозможно, то выходной файл должен содержать единственное число − 1.
Ограничения
1 ≤ N ≤ 1000, − 105 ≤ Xi, Yi, xi, yi ≤ 105.
Все числа во входном файле целые.
Примеры тестов
| № | Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|---|---|
| 1 | |
|
| 2 | |
|
Разбор
При решении задачи воспользуемся методом "разделяй и властвуй", т.е. будем на каждом шаге сводить решение исходной задачи к решению подзадачи меньшего размера.
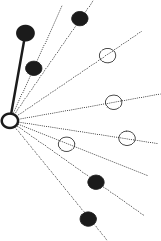
Вначале определим, с каким островом нужно соединять самый левый остров.
Для этого отсортируем все острова, кроме самого левого, по возрастанию полярного угла относительно него и пронумеруем их от 1 до N − 1. Будем считать, что самый левый остров высокий (случай, когда он низкий, рассматривается аналогично).
- Если остров с номером 1 низкий, то соединим его с самым левым островом, а затем повторим наш алгоритм для множества всех остальных островов.
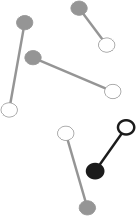
- Если остров с номером N − 1 низкий, то поступим точно так же, как в предыдущем случае (см. Рис. 1).
-
Если острова с номерами 1 и N − 1 высокие, то существует низкий остров с номером i, такой, что среди всех островов с номерами, меньшими i, высоких и низких островов поровну (см. Рис. 2). Тогда соединим i-й остров с самым левым. Затем повторим наш алгоритм сначала для островов с номерами 1, 2, ..., i − 1, а потом для островов с номерами i + 1, i + 2, ..., N − 1.
Докажем, что найдётся низкий остров с номером i, такой, что среди всех островов с номерами, меньшими i, высоких и низких островов поровну.
Рассмотрим последовательность чисел a1, a2, ..., aN − 1, в которой ak = 1, если остров с номером k низкий, и ak = − 1, если остров с номером k высокий.
Пусть Sk = a1 + a2 + ... + ak. Заметим, что SN − 1 = 1. Так как aN − 1 = − 1, то SN − 2 = 2. При этом S1 = − 1, причём Sk + 1 отличается от Sk ровно на 1.
Поэтому найдётся такое i, что 1 < i < N − 2 и Si = 1.
Если ai = 1, то i-й остров низкий и Si − 1 = 0, значит, среди островов с номерами 1, 2, ... i − 1 высоких и низких островов поровну, что и требовалось доказать.
Если же ai = − 1, то мы можем принять i за N − 1 (убрать лишние острова) и повторить рассуждения. В конце концов мы найдём искомое i.
На рисунке показан пример работы алгоритма.
Докажем, что алгоритм работает верно, когда количество островов равно N. Предположим по индукции, что алгоритм работает верно, т.е. строит не пересекающиеся мосты, когда количество островов меньше N.
Все мосты можно разделить на три класса.
- Мост, соединяющий самый левый остров с i-м.
- Мосты, построенные при первом дополнительном вызове алгоритма.
- Мосты, построенные при втором дополнительном вызове алгоритма.
Докажем, что любые два моста не пересекаются. Если оба моста принадлежат второму классу или оба моста принадлежат третьему классу, то они не пересекаются в силу нашего предположения, что алгоритм работает верно, когда количество островов меньше N.
Если один мост принадлежит второму классу, а другой - третьему классу, то они не пересекаются, потому что лежат по разные стороны от прямой, содержащей мост из первого класса.
По той же причине мост из первого класса не пересекается ни с каким мостом.
Итак, мосты не пересекаются друг с другом, поэтому алгоритм работает верно.