Задача T. Сердце горы ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 256 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
Хоббит и гномы наконец-то добрались до Одинокой горы. Логово Смауга имеет форму треугольника, высотой n этажей, и разбито на n2 равных пронумерованных треугольных комнат (смотри рисунок). Бильбо может свободно перемещаться между комнатами, соблюдая три правила:
1) нельзя подниматься на этаж выше того, на котором сейчас находишься;
2) нельзя возвращаться в комнату, в которой уже побывал.
3) можно переместиться в комнату, если она имеет общую сторону с той, в которой сейчас находишься, если это не противоречит предыдущим правилам.
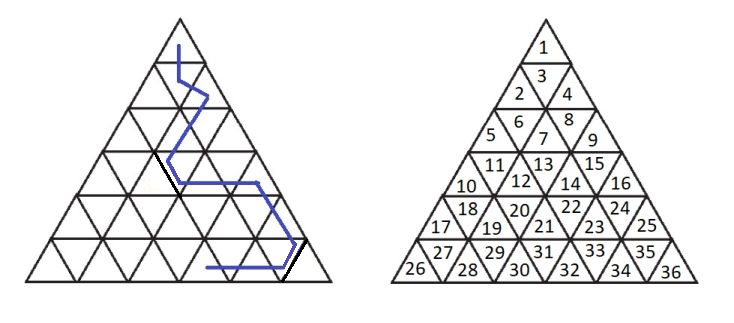
Для каждой комнаты известно количество золотых монет, находящихся в ней. Также в комнате номер d находится дракон. Вор-взломщик начинает в самой верхней комнате и заканчивает свой путь в любой из нижних (на рисунке слева изображен один из допустимых маршрутов). Какое наибольшее количество монет он сможет собрать? Естественно, маршрут хоббита не должен включать комнату с драконом.
Формат входных данных
Первая строка входного файла содержит натуральное число n. В следующей строке через пробел расположены n2 натуральных чисел xi — количество монет в i-й комнате. В третьей строке расположено натуральное число d.
Формат выходных данных
Выведите одно натуральное число — ответ на вопрос задачи.
Ограничения
2 ≤ n ≤ 100
1 ≤ xi ≤ 109
2 ≤ d ≤ 100
d ≠ 3
Система оценки и описание подзадач
Баллы за каждый тест начисляются независимо.
Решения, верно работающие при n = 2, получат не менее 10 баллов.
Решения, верно работающие при xi = 1, получат не менее 10 баллов.
Пояснение к примеру
В примере маршрут хоббита будет включать комнаты 1, 3, 4, 8 и 9. Если бы дракон находился в комнате 2, можно было бы собрать 34 монеты, посетив комнаты 1, 3, 4, 8, 7, 6 и 5
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|