Задача 74. И не друг, и не враг ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 64 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
Если друг оказался вдруг
И не друг, и не враг, а — так;
Если сразу не разберешь,
Плох он или хорош, —
Парня в горы тяни — рискни!
Не бросай одного его:
Пусть он в связке в одной с тобой —
Там поймешь, кто такой.
...
Владимир Высоцкий, "Песня о друге", 1966 г.
Не так давно на просторах Интернета появилась новая социальная сеть для альпинистов "На высоте". В результате обсуждений на форуме последних результатов в скалолазании, пользователи стали активно добавлять друг друга в "друзья" и "враги". Через некоторое время выяснилось, что если альпинист A добавил в друзья альпиниста B, то и B добавил A в друзья. И наоборот, если альпинист A добавил во враги альпиниста B, то и B считает A своим врагом. Кроме друзей и врагов для пользователей этой сети существуют и нейтральные "Высотники", причем это отношение тоже коммуникативное: если A относится нейтрально к B, то и B так же относится к A.
Спустя некоторое время модераторы форумов сети стали наблюдать тревожную тенденцию спада активности: у каждого пользователя образовался замкнутый круг общения. Чтобы "расшевелить" людей, администраторы сайта решили уменьшить количество нейтральных отношений и предложить альпинистам перевести из нейтральных в друзья тех пользователей, которые являются "врагами их врагов". Формально это можно описать так — если A нейтрален к B и существует хотя бы один C, для которого выполняется условие: A враг C и C враг B, то стоит предложить A добавить B в друзья.
Определите количество людей, которых предложат в качестве потенциальных друзей указанному пользователю социальной сети.
Формат входных данных
Первая строка входного файла содержит два натуральных числа, записанных через пробел: n — количество зарегистрированных пользователей и k — номер болельщика. В следующих n строках длины n в виде таблицы расположено описание отношений между болельщиками. Символ "f" соответствует отношению друг, "a" — враг, "n" — нейтральный. На пересечении строки и столбца с одинаковым номером находится символ "x". Гарантируется симметричность таблицы относительно главной диагонали.
Формат выходных данных
Выведите одно неотрицательное целое число — количество предложений добавить в друзья новых людей, которое получит пользователь с номером k.
Ограничения
1 ≤ k ≤ n ≤ 500
Система оценки и описание подзадач
Баллы за каждый тест начисляются независимо.
Решения, верно работающие при n ≤ 100, получат не менее 60 баллов.
Пояснение к примеру
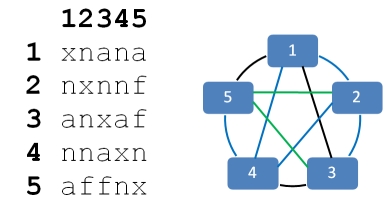
В примере первому пользователю будет предложено добавить в друзья четвертого пользователя — он нейтрален первому и существует альпинист (номер 3), являющийся их общим врагом. На рисунке внизу таблица отношений преобразована в граф. Зеленые линии обозначают дружбу, черные — вражду, синие — нейтральные отношения.
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|