Задача D. Коридор ≡
| Автор: | А. Жуплев | Ограничение времени: | 1 сек | |
| Входной файл: | input.txt | Ограничение памяти: | 64 Мб | |
| Выходной файл: | output.txt | |||
| Максимальный балл: | 100 |
Условие
Коридор размером N на M решили застелить покрытием, представляющим собой плитки размером 1 на M. Сколькими способами можно это сделать, если не должно быть не застеленной поверхности?
Для коридора с размерами N = 6 и M = 4, существуют 4 способа укладки плиток.
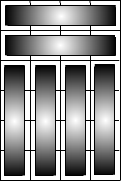

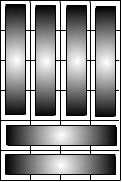
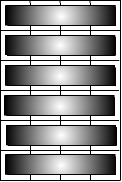
Формат входного файла
В первой строке входного файла содержатся числа N M.
Формат выходного файла
В выходном файле должно содержаться единственное число — количество различных способов, которыми можно застелить коридор.
Ограничения
2 ≤ N, M ≤ 50
Примеры тестов
| № | Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|---|---|
| 1 | |
|
| 2 | |
|
| 3 | |
|
Разбор
Задачу можно частично решить методом перебора всех возможных вариантов: на текущем шаге ставим или вертикальную или горизонтальную плитку и переходим к следующей итерации перебора. Когда приходим в состояние, в котором весь коридор застелен, увеличиваем ответ на единицу.
void rec(int i){
if(i == 0){
ans++; return;
}
if(i >= m) rec(i-m);
rec(i-1);
}
Такое решение набирало 50 баллов.
Чтобы решить задачу полностью, воспользуемся методом динамического программирования. a[i] = p будет означать, что коридор размером i на M можно застелить p способами.
На текущем шаге мы можем положить плитку либо вертикально a[i] или горизонтально a[i+m-1]. Ответом будет a[n]. Коридор размера 0 на M можно застелить одним способом — не застилать ничего.
a[0] = 1; for(i = 1; i < = n; i++){ if(i + m - 1 < = n) ans[i+m-1] += ans[i-1]; ans[i] += ans[i-1]; }