Задача A. Ёлочки 2 ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 64 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
Скоро Новый Год! А это значит, что на носу конец второй четверти и Тимофею самое время взяться за исправление отметок по рисованию. На сегодняшнем уроке весь класс рисует зимний лес. К сожалению, с передачей художественных образов изобразительными методами дела у Тимофея обстоят из рук вон плохо. Но хоть что-то нарисовать нужно, поэтому Тимофей рисует ёлочки по клеточкам.
Каждая елочка имеет свою красоту, равную количеству ветвей с одной стороны ствола и (так уж совпало) длине самой нижней ветви. Каждая следующая верхняя ветка на одну клетку короче предыдущей. Между ветвями, а также под самой нижней и над самой верхней ветвями находится ствол дерева шириной ровно в одну клетку. На рисунке вы видите ёлки кисти Тимофея красотой от 0 до 5 включительно.
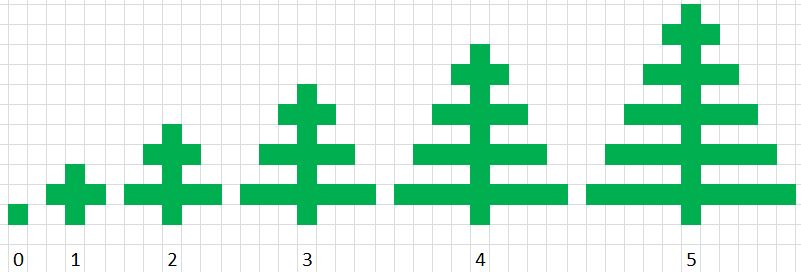
Поскольку с математическими формулами Тимофей дружит гораздо сильнее, чем с акварельными красками, его заинтересовал вопрос, какой периметр у клетчатой ёлки определенной красоты? Тимофей без труда решил эту задачу. А вы сможете?
Формат входных данных
В единственной строке записано одно неотрицательное целое число n - красота ёлки.
Формат выходных данных
Выведете одно натуральное число - периметр ёлки красоты n.
Ограничения
0 ≤ n ≤ 109
Система оценки и описание подзадач
Баллы за каждую подзадачу начисляются только в случае, если все тесты этой подзадачи успешно пройдены.
Подзадача 1: 0 ≤ n ≤ 105, баллы: 30.
Подзадача 2: нет дополнительных ограничений, баллы: 70.
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|