Задача C. VR-обсерватория ≡
| Автор: | А. Баранов | Ограничение времени: | 1 сек | |
| Входной файл: | input.txt | Ограничение памяти: | 256 Мб | |
| Выходной файл: | output.txt | |||
| Максимальный балл: | 100 |
Условие
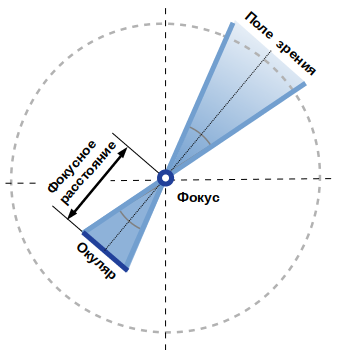
Молодой программист Вася занимается разработкой собственной VR-игры, представляющей собой симулятор астрономической обсерватории. Предполагается, что в ней игрок должен будет смотреть на звезды через окуляр круглой формы с фокусом, расположенным в начале координат.
В целях тестирования игровой механики Вася сгенерировал достаточно большое число трехмерных точек.
Теперь ему требуется для некоторого заданного направления обзора, фокусного расстояния и радиуса окуляра определить число всех таких точек, попадающих в его поле зрения.
При этом точки, расположенные между окуляром и фокусом, должны быть проигнорированы.
Формат входного файла
В начале входного файла "input.txt" записано натуральное число N, за которым следует ровно 3 ⋅ N координат точек (Xi, Yi, Zi).
Далее записано число M, за которым следует M запросов, каждый из которых задается вектором направления →Dj = (Uj, Vj, Wj) и радиусом Rj.
При этом полагается, что длина вектора →Dj соответствует фокусному расстоянию.
Формат выходного файла
Выходной файл "output.txt" должен содержать M целых чисел — ответы на каждый запрос.
Ограничения
Гарантируется, что суммарное число точек во всех запросах не превосходит 106.
Все входные значения являются целыми десятичными числами.
− 106 ≤ (Xi, Yi, Zi) ≤ 106, − 106 ≤ (Uj, Vj, Wj) ≤ 106, 0 < |→Dj|, 0 ≤ Rj ≤ 106
1 ≤ N ≤ 105, 1 ≤ M ≤ 105
Примеры тестов
| № | Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|---|---|
| 1 | |
|
Разбор
Как следует из условия задачи, от нас требуется искать точки, попадающие в некоторый бесконечный конус с вершиной, лежащей в начале координат.
В свою очередь, такой конус можно определить как множество лучей, которые отклоняются не более чем на угол Δ φ от заданного вектора D⃗.
Допустимый диапазон угла Δ φ может быть получен через соотношение tan(Δ φ) = R|D⃗|.
Вместо исходных точек будем рассматривать соответствующие им радиус-векторы P⃗ = (x, y, z).
Случай для точки (0, 0, 0) можно обработать отдельно. По этой причине здесь и далее будем полагать, что длины радиус-векторов не равны нулю.
Для отдельно взятой точки P⃗ можно найти угол φ через соотношение: cos(φ) = (P⃗ ⋅ D⃗)|P⃗||D⃗|.
Отметим, что во избежание погрешностей округления здесь желательно избавиться от использования тригонометрических функций и взятия корня.
Например, исключив точки, лежащие позади фокуса (P⃗ ⋅ D⃗ < 0), вместо углов мы можем рассматривать квадраты их косинусов:
tan2(Δ φ) = R2|D⃗|2;
cos2(Δ φ) = 1tan2(Δ φ) + 1;
cos2(φ) = (P⃗ ⋅ D⃗)2|P⃗|2|D⃗|2.
Наивное решение заключается в том, чтобы перебрать все существующие точки и для каждой из них проверить попадание в заданный конус.
Однако, учитывая общее число запросов, такой подход окажется весьма затратным по времени.
Для оптимизации по времени при многократно выполняемых запросах воспользуемся структурой BSP-дерева (Binary-Space-Partitioning Tree).
Суть его заключается в рекурсивном разбиении исходного набора точек таким образом,
чтобы на каждом шаге очередное подмножество делилось на две примерно равные части
относительно некоторой выбранной плоскости (в общем случае — поверхности).
Наиболее простым в реализации вариантом такой структуры является k-D дерево. Его идея заключается в следующем.
Вначале зафиксируем координату с номером l и расположим точки исходного множества в порядке ее возрастания.
Далее выберем среди них медиану P и припишем ее текущему узлу нашего дерева.
Оставшееся множество точек разобьем на две части: лежащие слева и справа от точки P.
Для каждого из полученных подмножеств выполняется аналогичная процедура.
Точки разбиения таких подмножеств будут размещены в левом и правом потомках исходного узла, соответственно.
Переходя между уровнями, будем чередовать координату l, обеспечивая разбиение по всем возможным направлениям.
Поиск точек, попадающих в некоторую заданную область, выполняется путем рекурсивного обхода полученного дерева.
При этом мы можем эффективно отсекать те из них, которые явно в нее не попадают,
проверяя положение заданной области относительно секущей поверхности
и уже по результатам такой проверки принимая решение, в каком из двух подмножеств следует продолжать поиск.
В общем же случае имеет смысл рассматривать некоторый бокс,
ограничивающий заданную область по каждой из осей координат.
В связи с этим возникает вопрос о выборе системы координат,
чтобы сформировать бокс, наилучшим образом приближающий исходную область.
Так, для конуса можно воспользоваться следующим подходом.
Очевидно, что длины исходных радиус-векторов не влияют на результат решения.Поэтому для них сразу можно выполнить нормировку.
Таким образом, все точки окажутся на поверхности сферы единичного радиуса.
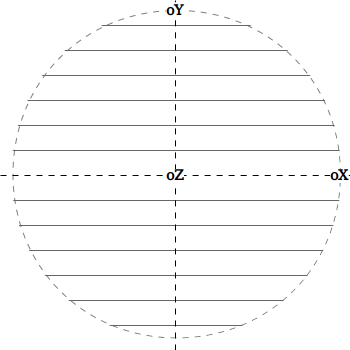
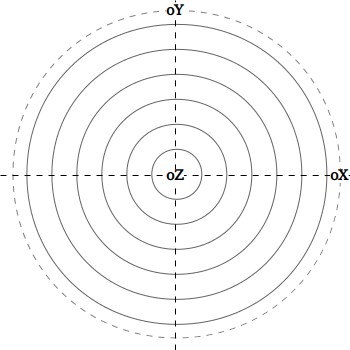
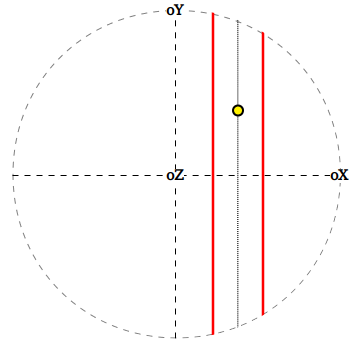
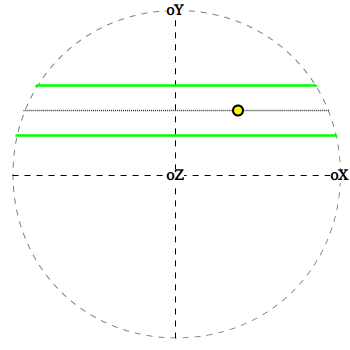
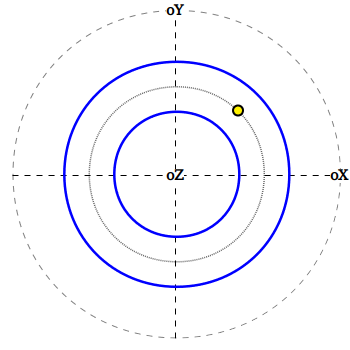
Рассмотрим углы отклонения точек от каждой из осей координат (oX, oY и oZ).
Значения углов будут лежать в диапазоне от 0 до π.
Точки, равноуклоненные от некоторой оси, формируют набор концентрических окружностей, лежащих на сфере.
В результате получим барицентрическую систему координат, где любая точка
сферы будет лежать на пересечении трех изоклин.
На рисунке можно видеть набор таких изоклин,
изображенных в проекции на плоскость XY.
 |
 |
 |
 |
| oX | oY | oZ |
Таким образом, каждая точка исходного множества может быть однозначно задана набором трех таких углов.
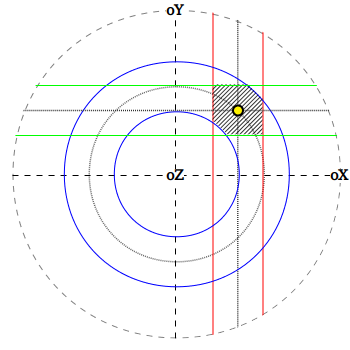
В свою очередь, ось нашего конуса также может
быть записана в новой системе координат.
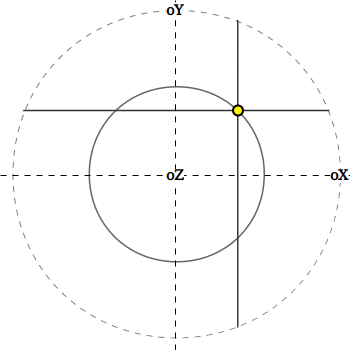
Также можно получить ограничивающий бокс,
в пределах которого лежит сам конус,
т.к. по каждому из возможных направлений отклонение по углу не должно превышать Δ φ.
Стоит отметить, что здесь ему будет соответствовать сферический шестиугольник
(заштрихованная область).
 |
 |
 |
 |
| oX | oY | oZ |
Таким образом, мы можем существенно сузить актуальную область поиска.
Все что остается, это проверить точки,
попадающие во внутрь такого бокса.