Задача A. Вписанный цилиндр ≡
| Автор: | А. Баранов | Ограничение времени: | 1 сек | |
| Входной файл: | input.txt | Ограничение памяти: | 256 Мб | |
| Выходной файл: | output.txt | |||
| Максимальный балл: | 100 |
Условие
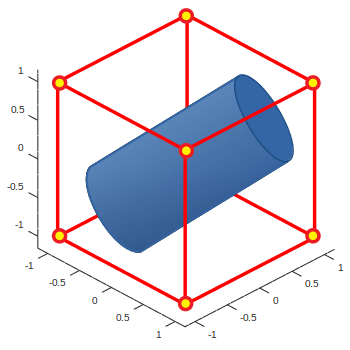
Пусть имеется некоторый выпуклый многогранник P и проходящая через него прямая L, заданная в параметрическом виде:
X(t) = X0 + t ⋅ UD, Y(t) = Y0 + t ⋅ VD, Z(t) = Z0 + t ⋅ WD, где D = √U2 + V2 + W2, t — произвольный скалярный параметр.
Требуется для некоторого заданного значения R определить цилиндр максимально возможной высоты
с осью L и радиусом R, целиком лежащий внутри многогранника P.
Формат входного файла
В начале входного файла "input.txt" записано число N, за которым следует 3 × N вещественных координат вершин.
Далее указано число M, за которым следует M граней, записанных в следующем виде.
Вначале для каждой грани указано число ее вершин, за которым следуют их индексы,
перечисленные в порядке их обхода для получения ограничивающего цикла грани.
При этом полагается, что нумерация вершин начинается с нуля.
В окончании входного файла указан набор вещественных значений:
X0, Y0, Z0, U, V, W, R.
Формат выходного файла
Если задача имеет решение, в выходной файл "output.txt" выводится число 1,
за которым следуют границы параметрического интервала,
задающего положение цилиндра на оси L,
указанные с точностью до 5-го знака после запятой
и расположенные в порядке возрастания.
В противном случае выходной файл должен содержать число 0.
Ограничения
Координаты всех вершин по модулю не превосходят 10.
Число вершин и граней не превосходит 100.
Прямая обязательно проходит сквозь внутреннюю
часть многогранника.
− 10 ≤ (X0, Y0, Z0, U, V, W) ≤ 10, 0 < R ≤ 10.
Гарантируется, что в пределах заданной
точности ответ может быть
получен однозначно.
Примеры тестов
| № | Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|---|---|
| 1 | |
|
Разбор
Для начала введем ряд обозначений: C1 = (X0, Y0, Z0) — начальная точка; L1 = (UD, VD, WD) — единичный вектор, задающий направление прямой.
Теперь любая точка, лежащая на оси цилиндра, может быть выражена параметрическим уравнением: C(t) = C1 + t ⋅ L1.
Обозначим за Ω(t) плоскость, проходящую через точку C(t) с нормалью L1.
Передвигая указанную плоскость по параметру t, будем изучать поперечные сечения цилиндра на предмет их выхода за пределы многогранника P.
Выпуклый многогранник может быть представлен в виде пересечения полупространств, ассоциированных с плоскостями соответствующих граней.
По этой причине будем последовательно перебирать грани многогранника.
Введем обозначения: C2 — произвольная точка, лежащая на грани; L2 — единичная внутренняя нормаль к грани.
Найдем вектор Q1 = L1 × L2, задающий направление прямой пересечения плоскости Ω с плоскостью грани,
и вектор Q2 = L1 × Q1, одновременно ортогональный как к оси цилиндра, так и к прямой пересечения.
В этом случае расстояние от точки C(t) до прямой пересечения будет вычисляться по направлению Q2.
Будем искать такой параметр p, при котором выполняется условие: ((C(t) + p ⋅ Q2) − C2) ⋅ L2 = 0.
Он соответствует точке, в которой прямая C(t) + p ⋅ Q2 пересекает плоскость грани.
В результате получим: p = − (C(t) − C2) ⋅ L2Q2 ⋅ L2; p = − t ⋅ L1 ⋅ L2Q2 ⋅ L2 − (C1 − C2) ⋅ L2Q2 ⋅ L2.
Упростим запись, введя вспомогательные обозначения: p = − t ⋅ L1 L2Q2 L2 − C12 L2Q2 L2.
Теперь выразим параметр t через p: t = − p ⋅ Q2 L2L1 L2 − C12 L2L1 L2.
Обратим внимание, что нас интересует возможность отступить от точки C(t), лежащей на оси цилиндра, по направлению Q2 на величину радиуса R.
При этом параметр p может принимать как положительные, так и отрицательные значения.
Определим границы интервала для t, на котором параметр p попадает в интервал [ − R, R]:
t1 = R ⋅ Q2 L2L1 L2 − C12 L2L1 L2;
t2 = − R ⋅ Q2 L2L1 L2 − C12 L2L1 L2.
Расположив полученные значения в порядке возрастания, получим интервал [t1, t2], на котором цилиндр пересекает плоскость грани.
При этом у нас останется два интервала ( − ∞, t1] и [t2, + ∞).
Чтобы выбрать из них нужный вспомним, что исходная прямая проходит через внутреннюю часть многогранника.
А значит, точка C(t) должна оказаться внутри соответствующего полупространства:
(C(t) − C2) ⋅ L2 ≥ 0.
По этой причине выбираем интервал, удовлетворяющий данному условию.
Решая указанную задачу для всех существующих граней, будем искать пересечение полученных интервалов.
Стоит также отметить, что в процессе решения могут возникать следующие особые случаи.
Первый случай возникает, когда плоскость грани ортогональна оси цилиндра |Q1| ≈ 0.
В этом случае, определим параметр t0, при котором ось цилиндра пересекает грань: t0 = − (C1 − C2) ⋅ L2L1 ⋅ L2,
и выбираем среди двух интервалов ( − ∞, t0] и [t0, + ∞).
Второй случай связан с ситуацией, когда грань параллельна оси цилиндра: L1 ⋅ L2 ≈ 0.
В этом случае достаточно проверить расстояние до плоскости грани,
т.к. при всех возможных значениях t оно меняться не будет.
Попадание в нужное полупространство здесь проверять не надо,
т.к. по условию ось цилиндра всегда проходит через
внутреннюю часть многогранника.