Задача A. Вписанный цилиндр ≡
| Автор: | А. Баранов | Ограничение времени: | 1 сек | |
| Входной файл: | input.txt | Ограничение памяти: | 256 Мб | |
| Выходной файл: | output.txt | |||
| Максимальный балл: | 100 |
Условие
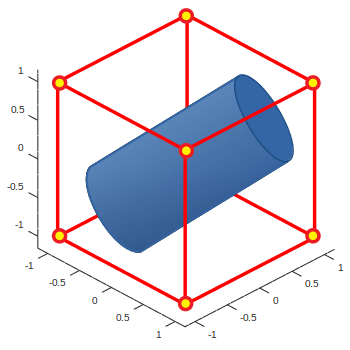
Пусть имеется некоторый выпуклый многогранник P и проходящая через него прямая L, заданная в параметрическом виде:
X(t) = X0 + t ⋅ UD, Y(t) = Y0 + t ⋅ VD, Z(t) = Z0 + t ⋅ WD, где D = √U2 + V2 + W2, t — произвольный скалярный параметр.
Требуется для некоторого заданного значения R определить цилиндр максимально возможной высоты
с осью L и радиусом R, целиком лежащий внутри многогранника P.
Формат входного файла
В начале входного файла "input.txt" записано число N, за которым следует 3 × N вещественных координат вершин.
Далее указано число M, за которым следует M граней, записанных в следующем виде.
Вначале для каждой грани указано число ее вершин, за которым следуют их индексы,
перечисленные в порядке их обхода для получения ограничивающего цикла грани.
При этом полагается, что нумерация вершин начинается с нуля.
В окончании входного файла указан набор вещественных значений:
X0, Y0, Z0, U, V, W, R.
Формат выходного файла
Если задача имеет решение, в выходной файл "output.txt" выводится число 1,
за которым следуют границы параметрического интервала,
задающего положение цилиндра на оси L,
указанные с точностью до 5-го знака после запятой
и расположенные в порядке возрастания.
В противном случае выходной файл должен содержать число 0.
Ограничения
Координаты всех вершин по модулю не превосходят 10.
Число вершин и граней не превосходит 100.
Прямая обязательно проходит сквозь внутреннюю
часть многогранника.
− 10 ≤ (X0, Y0, Z0, U, V, W) ≤ 10, 0 < R ≤ 10.
Гарантируется, что в пределах заданной
точности ответ может быть
получен однозначно.
Примеры тестов
| № | Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|---|---|
| 1 | |
|