Задача E. Конь-диверсант ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 256 Мб | |
| Выходной файл: | Стандартный выход |
Условие
На обычной шахматной доске 8×8 находится один белый конь и несколько черных ферзей. Конь может перемещаться по обычным правилам, но не может занять поле, если оно находится под боем ферзя. Однако, он может "съесть" ферзя, при условии, что тот не находится под защитой другого ферзя, получив, таким образом, дополнительные поля для перемещения (при этом, у него сохраняется возможность "съесть" ещё какого-нибудь ферзя). Теоретически, если ферзи не защищают друг друга, конь может съесть их всех и без помех "гулять" по всей шахматной доске. На скольких полях сможет побывать конь при данной расстановке?
Формат входных данных
Первая строка входных данных содержит одно натуральное число n — количество фигур на доске. Во второй строке через пробел приведено n двузначных чисел — координаты фигур. Первые n−1 чисел соответствуют расстановке ферзей, последнее — коня. Первая цифра числа — номер вертикали, вторая — горизонтали шахматного поля. Гарантируется, что координаты всех фигур различны. Гарантируется, что конь в начальном расположении не находится под боем.
Формат выходных данных
Выведите одно натуральное число — количество различных полей шахматного поля, до которых может добраться конь (включая исходное).
Ограничения
3≤n≤10
Пояснение к примеру
Смотри рисунок. Начальное положение фигур слева. Два ферзя на полях 15 и 48 защищают друг друга, съесть их нельзя, также нельзя перемещаться на те поля, которые находятся под их боем. Ферзь на поле 83 может быть съеден конем первым же ходом. Справа красными значками отмечены поля, находящиеся под боем ферзей, которых конь не сможет съесть. Зелеными значками отмечены поля, до которых конь может добраться. Вместе с исходным полем, всего их 24.
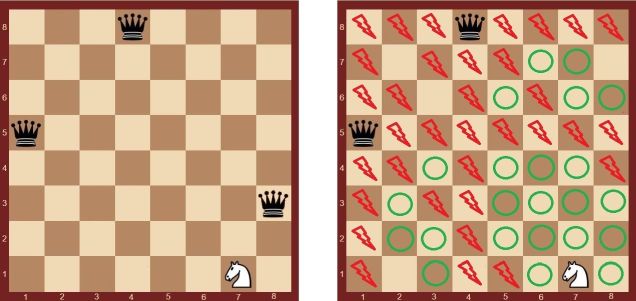
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|