Задача B. Пара парабол ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 64 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
На координатной плоскости две параболы заданы так, что линии их графиков образуют замкнутую область. У одной параболы ветви направлены вверх, а у другой вниз. Для заданной точки определите, попадает ли она в замкнутую область.
Формат входных данных
Первая строка входного файла содержит три целых числа, записанных через пробел: a1, b1 и c1 — коэффициенты первой квадратичной функции. Во второй строке в том же формате содержатся ещё три целых числа: a2, b2 и c2 — коэффициенты второй квадратичной функции. В третьей строке через пробел расположены два целых числа x и y — координаты точки. Гарантируется, что параболы, являющиеся графиками данных функций образуют на плоскости непустую замкнутую область.
Формат выходных данных
Выведите "Yes" или "No" (без кавычек) — ответ на поставленный вопрос. Если точка попадает на границу области, выведите "Yes".
Ограничения
−10≤a1,b1,c1,a2,b2,c2,x,y≤10
0<a1
a2<0
Система оценки и описание подзадач
Баллы за каждый тест начисляются независимо.
Пояснение к примеру
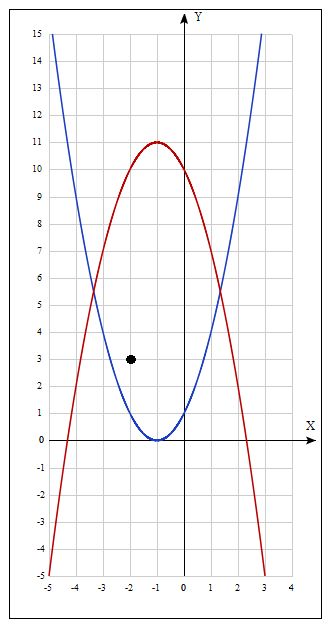
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|