Задача A. Equidistant shell ≡
| Автор: | A. Baranov | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 256 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
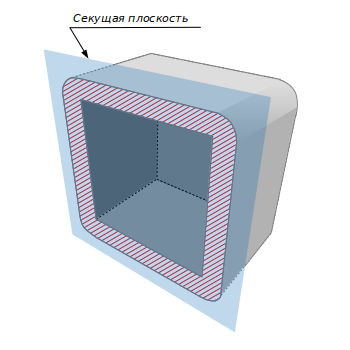
Эквидистантной оболочкой трехмерного тела называется множество внешних по отношению к нему точек, удаленных от него не более чем на заданное расстояние δ. На рисунке можно видеть пример эквидистантной оболочки для куба, представленной в разрезе.
Даны произвольный выпуклый многогранник и значение δ. Требуется написать программу, вычисляющую объем эквидистантной оболочки.
Формат входных данных
В начале входных данных хранится исходный многогранник, записанный в следующем виде.
Вначале идет целое число V, за которым следует ровно 3 ⋅ V вещественных чисел, задающих координаты вершин.
Далее целое число E, за которым следует ровно 2 ⋅ E номеров вершин, попарно задающих ребра.
Далее идет целое число F, за которым следует ровно F граней, записанных в следующем виде.
Вначале целое число ребер N, за которым следует N номеров ребер этой грани в произвольном порядке.
Нумерация всех указанных элементов начинается с нуля.
В конце входных данных записано вещественное значение δ.
Формат выходных данных
Выходные данные должны содержать объем с точностью не менее 5 знаков после запятой.
Ограничения
Все грани являются невырожденными и выпуклыми.
Координаты вершин лежат в диапазоне от − 10 до 10.
Число элементов каждого вида не превосходит 100.
0 ≤ δ ≤ 1
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|
Разбор
Для начала разложим оболочку исходного тела на составляющие.
Построим призмы высоты δ, путем вытягивания многоугольных граней в направлении их внешних нормалей.
Выберем нормали двух граней, стыкующихся по ребру.
Несложно убедиться, что проведенная через них плоскость будет ортогональна соответствующему ребру.
Построим цилиндры радиуса δ, оси которых совпадают с ребрами исходного многогранника,
а основания представляют собой сектора, проведенные между соответствующими нормалями.
Оставшиеся части оболочки примут вид шаровых секторов с центрами в вершинах исходного многогранника,
в основании которых лежат сферические многоугольники, центральные углы которых соответствуют
углам между нормалями смежных граней, сходящихся в текущих вершинах:
Несложно убедиться, что объединение всех указанных частей дает нам исходную оболочку.
В свою очередь, выпуклость исходного многогранника гарантирует,
что никакие две части не пересекаются между собой.
Таким образом, объем эквидистантной оболочки, может быть получен как сумма объемов указанных частей.
Объем каждой призмы будет равен Vp = Sp ⋅ δ, где Sp — площадь плоской грани.
Объем цилиндра будет равен Vc = Sc ⋅ |E|, где Sc — площадь сектора,
|E| — длина соответствующего ребра.
Можно попробовать доказать, что для выпуклого многогранника сумма объемов шаровых секторов
равна объему полного шара радиуса δ,
т.е. V = 4π ⋅ δ3 / 3.
С другой стороны, можно найти объем каждого такого сектора,
как Vs = Ss ⋅ δ / 3,
где Ss — площадь сферического многоугольника,
для нахождения которой можно воспользоваться
известной формулой.