Problem B. Binary Operation ≡
| Author: | ACM ICPC NEERC 2010 Jury | Time limit: | 2 sec | |
| Input file: | binary.in | Memory limit: | 256 Mb | |
| Output file: | binary.out |
Statement
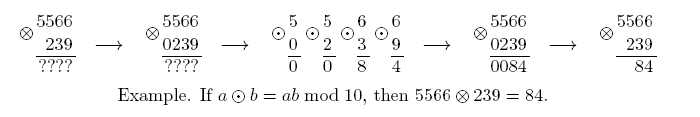 Consider a binary operation \op defined on digits 0 to 9, \op:\digs×\digs→\digs, such that 0\op0=0.
Consider a binary operation \op defined on digits 0 to 9, \op:\digs×\digs→\digs, such that 0\op0=0.
A binary operation \opd is a generalization of \op to the set of non-negative integers, \opd:\nneg×\nneg→\nneg. The result of a\opdb is defined in the following way: if one of the numbers a and b has fewer digits than the other in decimal notation, then append leading zeroes to it, so that the numbers are of the same length; then apply the operation \op digit-wise to the corresponding digits of a and b.
Let us define \opd to be left-associative, that is, a\opdb\opdc is to be interpreted as (a\opdb)\opdc.
Given a binary operation \op and two non-negative integers a and b, calculate the value of \res.
Input file format
The first ten lines of the input file contain the description of the binary operation \op. The i-th line of the input file contains a space-separated list of ten digits — the j-th digit in this list is equal to (i−1)\op(j−1).
The first digit in the first line is always 0.
The eleventh line of the input file contains two non-negative integers a and b (0≤a≤b≤1018).
Output file format
Output a single number — the value of \res without extra leading zeroes.
Sample tests
| No. | Input file (binary.in) |
Output file (binary.out) |
|---|---|---|
| 1 | |
|