Задача C. Взвешивание матрёшек ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 256 Мб | |
| Выходной файл: | Стандартный выход |
Условие
У Тимофея есть набор матрёшек, пронумерованных последовательными числами от 1 до n. Вес каждой матрёшки равен её номеру и любую матрёшку с номером a можно спрятать в матрёшку с номером b, если a < b.
Сегодня Тимофею удалось разместить все n матрёшек на равноплечных весах, так, что весы находятся в равновесии, а на их чашах видны всего две матрёшки, по одной на каждой чаше. Проверьте, не схитрил ли он.
Формат входных данных
Первая строка входных данных содержит натуральное число n — количество матрёшек у мальчика и одновременно номер матрёшки, стоящей на левой чаше весов. Вторая строка содержит натуральное число m — номер матрёшки, стоящей на правой чаше весов.
Формат выходных данных
Выведите True или False — ответ на вопрос, возможно ли расставить все n матрёшек описанным образом.
Ограничения
1 ≤ m < n ≤ 109
Пояснения к примерам
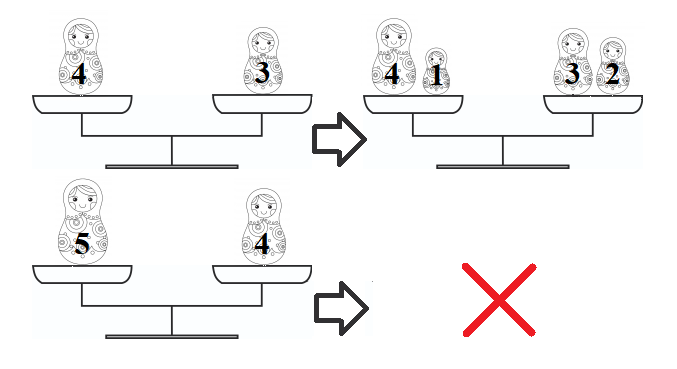
Смотри рисунок. В первом примере на левой чаше стоит матрёшка с номером 4, на правой — с номером 3.
Если в левую матрёшку спрятать матрёшку с номером 1, а в правую — с номером 2, то все четыре матрёшки окажутся на весах и весы будут находиться в равновесии.
Во втором примере на левой чаше стоит матрёшка с номером 5, на правой — с номером 4.
Из восьми способов расположения остальных матрёшек на двух чашах ни один не даёт требуемого равновесия:
1) 5 + 3 + 2 + 1 ≠ 4
2) 5 + 3 + 2 ≠ 4 + 1
3) 5 + 3 + 1 ≠ 4 + 2
4) 5 + 3 ≠ 4 + 2 + 1
5) 5 + 2 + 1 ≠ 4 + 3
6) 5 + 2 ≠ 4 + 3 + 1
7) 5 + 1 ≠ 4 + 3 + 2
8) 5 ≠ 4 + 3 + 2 + 1
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|
| 2 | |
|