Задача E. В деревне Гадюкино - дожди ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 64 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
На деревню Гадюкино надвигается n дождевых фронтов. Каждый фронт представляет собой отрезок на координатной плоскости и задается координатами начала x1,y1, конца x2,y2 и вектором направления (a,b) перемещения. Сколько дождевых фронтов пройдет через деревню Гадюкино, которая на координатной плоскости расположена в начале координат?
Формат входных данных
Первая строка входного файла содержит одно натуральное число n. В каждой из следующих n строк через пробел расположены шесть целых чисел x1, y1, x2, y2, a и b - описание очередного дождевого фронта. Гарантируется, что у каждого отрезка координаты начала и конца различны, а также, что вектор направления ненулевой.
Формат выходных данных
Выведите одно неотрицательное целое число - ответ на задачу. Считается, что дождевой фронт пройдет через деревню Гадюкино, если любая точка отрезка при его перемещении совпадет с началом координат.
Ограничения
1≤n≤100
−100≤x1,y1,x2,y2,a,b≤100
Система оценки и описание подзадач
Баллы за каждый тест начисляются независимо.
Решения, верно работающие при n=1, получат не менее 20 баллов.
Решения, верно работающие при a=0, получат не менее 20 баллов.
Пояснение к примеру
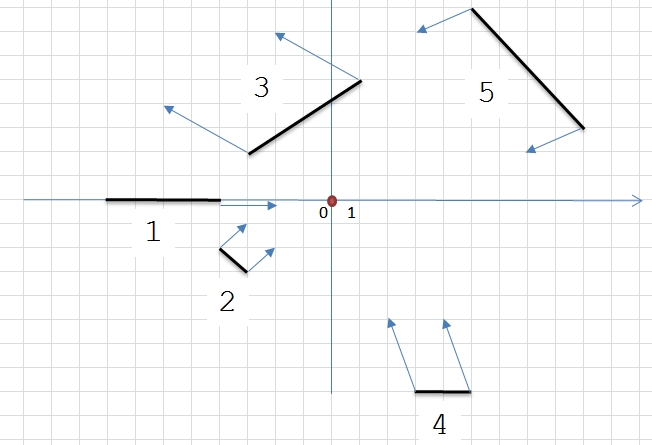
В примере даны пять дождевых фронтов.
Первый фронт пройдет через деревню.
Второй фронт заденет деревню одним из своих концов.
Третий фронт удаляется от деревни - дождя не будет.
Четвертый фронт чуть-чуть промахнется мимо деревни - дождя не будет.
Пятый фронт пройдет через деревню. Итого - три дождевых фронта.
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|