Задача B. Из пункта A в пункт B ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 64 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
В государстве, карту которого сейчас рисует Тимофей, все города представлены точками на координатной плоскости. Для организации транспортной системы Тимофей придумал очень интересную систему дорог (см. рисунок). Из одного города в другой можно добраться только по этим дорогам. Определите длину пути между двумя городами.
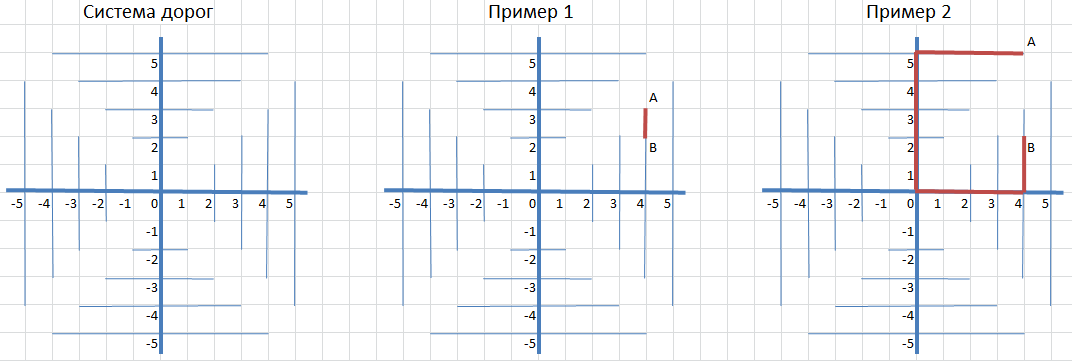
Формат входных данных
В единственной строке входного файла через пробел записаны четыре целых числа: x1, y1, x2, y2 – координаты первого и второго города соответственно. Гарантируется, что города не совпадают и ни один город не лежит в точке, для которой |x| = |y|.
Формат выходных данных
Выведите одно натуральное число - длину кратчайшего пути между городами.
Ограничения
− 109 ≤ x1, y1, x2, y2 ≤ 109
Система оценки и описание подзадач
Баллы за каждую подзадачу начисляются только в случае, если все тесты этой подзадачи успешно пройдены.
Подзадача 1: x1 = x2, |y1| ≤ |x1|, |y2| ≤ |x2|, баллы: 30.
Подзадача 2: нет ограничений, баллы: 70.
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|
| 2 | |
|