Задача A. Мишень ≡
| Входной файл: | input.txt | Ограничение времени: | 1 сек | |
| Выходной файл: | output.txt | Ограничение памяти: | 512 Мб | |
| Максимальный балл: | 100 |
Условие
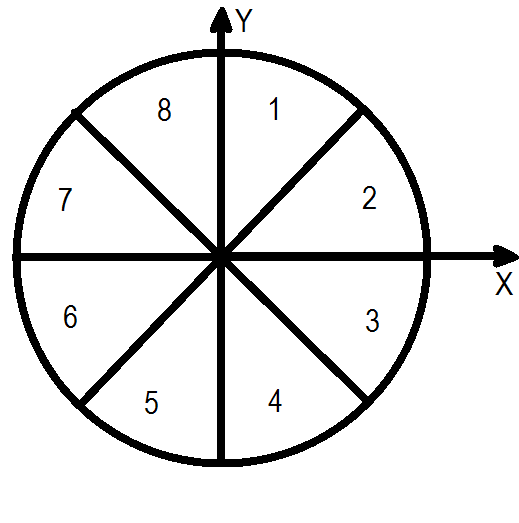
Вы реализуете игру "дартс" в виртуальной реальности. Игра устроена следующим образом. Дана мишень в форме круга радиуса R, расположенная в плоскости XY с центром в координатах (0, 0), разбитая на n равных секторов. Сектора пронумерованы от 1 до n по часовой стрелке. В момент броска мишень находится в таком положении, что сегмент с номером 1 расположен в верхней полуплоскости справа от оси Y. Мишень закручивается вокруг оси Z по часовой стрелке и приобретает постоянную угловую скорость w градусов в секунду.
Игрок, стоя лицом к мишени на расстоянии z, бросает дротик из координаты (x, y) в плоскости XY перпендикулярно мишени в её сторону. Дротик летит прямолинейно с постоянной скоростью v, не изменяя высоту полёта.
Требуется написать программу, которая определяет номер сектора, в который попадёт игрок.
Формат входного файла
Входные данные содержат целые числа R, w, x, y, z, v, n. Гарантируется, что участник не попал в границу между секторами.
Формат выходного файла
Выходные данные должны содержать единственное целое число — номер сектора, в который попал участник, или 0, если участник не попал в мишень.
Ограничения
1 ≤ r, w, v, z ≤ 100
− 100 ≤ x, y ≤ 100
2 ≤ n ≤ 100
Примеры тестов
| № | Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|---|---|
| 1 | |
|
| 2 | |
|
Разбор
Для того что проверить попадёт ли игрок в мишень достаточно проверить следующее условие: R2 ≤ x2 + y2.
Для вычисления времени полёта дротика до мишени используем формулу t = z / v. Используем формулу Rotation = w ⋅ t для того, чтобы узнать, на сколько градусов повернётся мишень во время полёта дротика.
Далее вычислим угол StartAngle к оси координат OX радиус-вектора (x, y). Для удобства повернём StartAngle на − π / 2. StartAngle = atan2(y, x) − π / 2.
Посчитаем конечный угол в радианах: ResultAngle = StartAngle + Rotation / 360 ⋅ 2 ⋅ π.
Преобразуем угол ResultAngle так, чтобы он лежал в диапазоне от 0 до 2 ⋅ π.
Размер одного сектора OneSector = 2 ⋅ π / n. Тогда искомый индекс n − ⌊ ResultAngel / OneSector⌋.