Задача 3. Треугольная головоломка ≡
| Входной файл: | Стандартный вход | Ограничение времени: | 1 сек | |
| Выходной файл: | Стандартный выход | Ограничение памяти: | 512 Мб | |
| Максимальный балл: | 100 |
Условие
Головоломка состоит из n треугольников. Чтобы решить головоломку, необходимо выбрать из них четыре треугольника и собрать из них большой треугольник по следующей схеме:
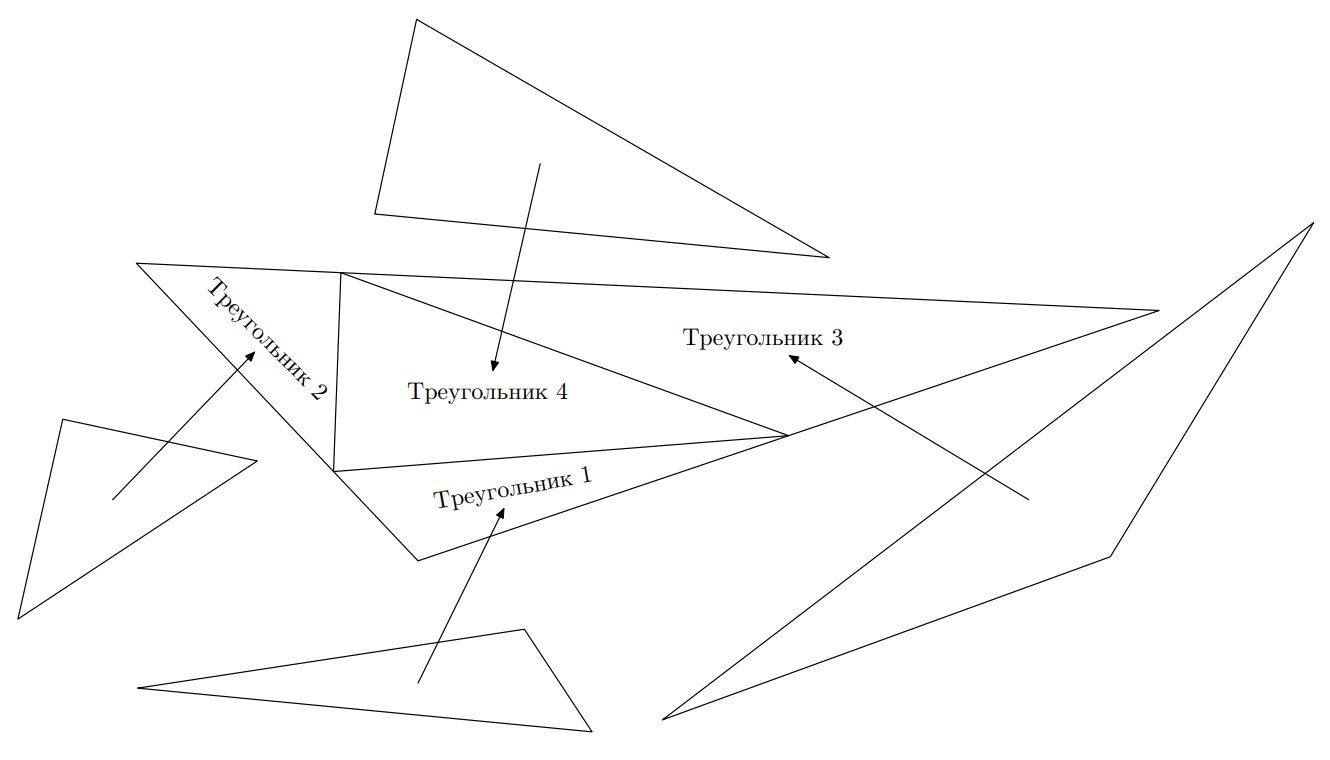
Треугольники не должны пересекаться, в объединении они должны давать треугольник. Ровно по одному из выбранных треугольников должны находиться в углах, а один треугольник должен располагаться в центре.
Треугольники лежат на столе, их можно свободно вращать и двигать, но нельзя зеркально отражать.
Формат входных данных
В первой строке дано одно целое число t — номер теста.
В второй строке дано одно целое число n — количество треугольников в головоломке (4≤n≤30).
В следующих n строках дано описание треугольников. Один треугольник описывается координатами трех своих углов, данных в порядке обхода треугольника против часовой стрелки. Все координаты по модулю не превышают 105. Гарантируется, что треугольники не являются вырожденными. В исходном расположении треугольники могут пересекаться.
Формат выходных данных
В первой строке выведите одно целое число — количество наборов из четырех треугольников, из которых можно собрать большой треугольник по указанной схеме.
В следующих строках выведите наборы. Каждый набор задается номерами треугольников, которые в него входят. Треугольники внутри набора можно выводить в любом порядке. Наборы можно выводить в любом порядке.
Ограничения
Система оценки
В этой задаче потестовая оценка. Каждый тест оценивается независимо и стоит 5 баллов.
Тесты удовлетворяют следующим ограничениям:
| Тест | Описание теста |
|---|---|
| 1 | тест из примера, не оценивается |
| 2 | тест из примера, не оценивается |
| 3 | Все треугольники равны с точностью до поворота, n≤30 |
| 4 | У каждого треугольника есть горизонтальная и вертикальная стороны, все треугольники равнобедренные, n≤10 |
| 5 | У каждого треугольника есть горизонтальная и вертикальная стороны, все треугольники равнобедренные, n≤30 |
| 6 | У каждого треугольника есть горизонтальная и вертикальная стороны, n≤10 |
| 7 | У каждого треугольника есть горизонтальная и вертикальная стороны, n≤30 |
| 8 | Все треугольники прямоугольные, n≤10 |
| 9 | Все треугольники прямоугольные, n≤30 |
| 10 | Для каждой четверки треугольников, из которой можно собрать треугольник, гарантируется, что треугольник можно собрать не вращая треугольники, n≤10 |
| 11 | Для каждой четверки треугольников, из которой можно собрать треугольник, гарантируется, что треугольник можно собрать не вращая треугольники, n≤20 |
| 12 | Для каждой четверки треугольников, из которой можно собрать треугольник, гарантируется, что треугольник можно собрать не вращая треугольники, n≤30 |
| 13 | n=10 |
| 14 | n=10 |
| 15 | n=10 |
| 16 | n=20 |
| 17 | n=20 |
| 18 | n=20 |
| 19 | n=30 |
| 20 | n=30 |
| 21 | n=30 |
| 22 | n=30 |
Пояснение к примеру
В первом примере из данных четырех треугольников можно собрать один. При этом треугольники не требуется вращать.
Во втором примере все треугольники имеют одинаковую форму прямоугольного треугольника с длинами катетов равными 1. Из любых четырех треугольников можно собрать один.
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|
| 2 | |
|