Problem I. Image correction ≡
| Author: | A. Baranov | Time limit: | 1 sec | |
| Input file: | Standard input | Memory limit: | 256 Mb | |
| Output file: | Standard output |
Statement
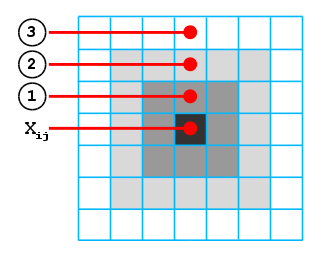
Matrix of camera represents a rectangular table of dimensions [n × m], consisting of photosensitive elements (cells). At the moment of shooting, each cell of this table is assigned a real value Xi j, indicating its state (intensity).
It is known that when reading the state of a particular cell, a weighted sum of the states of the surrounding cells is added to it, forming an ordered set of layers (see the figure). In this case, each subsequent layer has half the influence of the previous one.
The influence coefficient of each such cell on the obtained value is equal to 1 / (2l ⋅ Nl), where l is the number of the layer containing it, and, Nl is the number of cells in the l-th layer.
Also, for a separately taken camera model, the maximum number of layers k, influencing the measurement result is known.
For a given matrix Y, obtained as a result of measurements and an impact radius k it is required to restore the original values Xi j.
The values of dummy cells (located outside the matrix) are considered to be zero.
Input format
At the beginning of the input data three natural numbers are stored: n, m и k. Then follows the matrix of measurement results Y, recorded in row format.
Output format
The output data should contain the restored matrix X. All values should be specified with an accuracy of up to 5 decimal places.
Constraints
0 ≤ Yi j ≤ 10, 0 < n ⋅ m ≤ 40 000, 0 < k ≤ 6
Sample tests
| No. | Standard input | Standard output |
|---|---|---|
| 1 | |
|