Задача C. Баскетбол ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 64 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
Тимофей с одноклассниками обожают играть в баскетбол и не пропускают ни одной возможности сыграть в эту замечательную игру. Вот и сегодня на большой перемене состоялась важная игра (за выход в 1/1024 финала Объединенного городского школьного турнира).
Игра начинается со счета 0:0. Каждая результативная атака может принести одной из двух команд 1, 2 или 3 очка.
Введем понятие "ход игры" — последовательность изменения счета на табло. Например, ход игры может быть таким: 0-0, 2-0, 2-1, 5-1, 5-3.
Когда учитель информатики по пути в учительскую заглянул в спортзал, счет на табло был a:b. А после звонка на урок был зафиксирован окончательный результат — счет c:d. Теперь на уроке информатики перед ребятами поставлена задача — определить, сколько существует ходов игры, в которых:
1) Начальный счет — 0:0;
2) Промежуточный счет — a:b;
3) Окончательный счет — c:d.
Помогите Тимофею и его одноклассникам!
Формат входных данных
В первой строке входного файла через пробел записаны два числa: a и b — промежуточный счет. Во второй строке входного файла через пробел записаны два числa: c и d — окончательный счет.
Формат выходных данных
Выведите одно натуральное число — количество различных ходов игры. Гарантируется, что ответ на задачу при любых входных данных не превосходит 1018.
Ограничения
0 ≤ a ≤ c ≤ 20 и 0 ≤ b ≤ d ≤ 20
Система оценки и описание подзадач
Баллы за каждую подзадачу начисляются только в случае, если все тесты этой подзадачи успешно пройдены.
Подзадача 1: a = 0, b = 0, c = 0, баллы: 15.
Подзадача 2: a = 0, c = 0, баллы: 15.
Подзадача 3: a = 0, b = 0, c = 1, баллы: 20.
Подзадача 4: a = 0, b = 0, баллы: 20.
Подзадача 5: нет ограничений, баллы: 30.
Пояснения к примерам
Комментарий ко второму примеру:
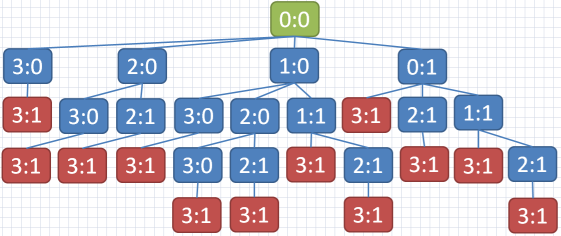
Комментарий к третьему примеру:

Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|
| 2 | |
|
| 3 | |
|