Problem B. Bouncing particles ≡
| Author: | A. Baranov | Time limit: | 1 sec | |
| Input file: | Standard input | Memory limit: | 256 Mb | |
| Output file: | Standard output |
Statement
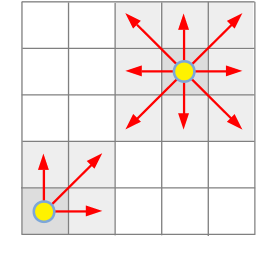
Suppose there is a rectangular area divided into N × M square cells. Some of these cells have particles.
In one time step, each particle can either stay in place or move to any of its neighboring cells.
It is required to count the number of possible particle movements, such that after L steps, they all end up in the same cell.
Since the obtained number may be too large, the answer should be the remainder when dividing it by (232 − 5).
Input format
At the beginning of the input data there is a triplet of numbers N, M и L.
Then, the number K is specified, followed by a set of 2 × K indices of the starting cells: Xi, Yi.
It is assumed that cell indexing starts from zero.
Output format
The output data should contain the obtained number.
Constraints
1 ≤ N ⋅ M ≤ 2 500, 0 ≤ L ≤ 50, 2 ≤ K ≤ 50, 0 ≤ Xi < N, 0 ≤ Yi < M.
Sample tests
| No. | Standard input | Standard output |
|---|---|---|
| 1 | |
|
| 2 | |
|