Задача D. Полное прохождение ≡
| Автор: | А. Усманов | Ограничение времени: | 2 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 256 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
Этим летом у Анастасии было много свободного времени, и она решила пройти все уровни своей любимой компьютерной игры. Для полного прохождения одного уровня требуется пройти все его эпизоды.
Сегодня Анастасия будет проходить уровень, состоящий из N эпизодов. Некоторые из эпизодов можно пройти на разную концовку, из-за которой определяется следующий эпизод в уровне. При этом некоторые эпизоды являются конечными — у таких нет следующего эпизода. На каждый эпизод, кроме первого — начального, можно попасть ровно из одного другого эпизода. Более формально иерархию эпизодов можно описать подвешенным деревом из N вершин.
После прохождения некоторых эпизодов, на них можно будет сохраниться, и в следующий раз продолжить прохождения с начала этих эпизодов. Всего есть M эпизодов с возможностью сохранения, причем в первом эпизоде точно можно сохраняться.
Анастасии стало интересно, какое минимальное количество эпизодов ей надо пройти для полного прохождения этого уровня.
Требуется написать программу, которая по описанию уровня определит минимально возможное количество эпизодов, которые нужно пройти для полного прохождения этого уровня.
Формат входных данных
Первая строка содержит два целых числа N и M — количество эпизодов в уровне и количество эпизодов, на которых можно сохраняться, соответственно.
Вторая строка содержит M различных целых чисел ai — номера эпизодов в игре, на которых действует сохранение.
Далее следует N − 1 строк, i из которых содержит два целых числа ui и vi — эпизод, который нужно пройти, и эпизод, на который можно попасть после этого, соответственно.
Гарантируется, что иерархия эпизодов описывает подвешенное дерево.
Гарантируется, что на 1 уровне можно сохраняться.
Формат выходных данных
В единственной строке выведите ответ на задачу.
Ограничения
1 ≤ M ≤ N ≤ 105
1 ≤ ai, ui, vi ≤ N
Описание подзадач и системы оценивания
Баллы за каждую подзадачу начисляются только в случае, если все тесты этой подзадачи и необходимых подзадач успешно пройдены.
Проверка каждой подзадачи выполняется до первой ошибки на каком-нибудь тесте этой подзадачи.
По запросу сообщается результат окончательной проверки на каждом тесте.
| Подзадача | Баллы | Дополнительные ограничения | Необходимые подзадачи | |
|---|---|---|---|---|
| N | M | |||
| 1 | 16 | 1 ≤ N ≤ 102 | 1 ≤ M ≤ N | |
| 2 | 15 | 1 ≤ N ≤ 104 | 1 ≤ M ≤ N | 1 |
| 3 | 23 | 1 ≤ N ≤ 105 | M = 1 | |
| 4 | 22 | 1 ≤ N ≤ 105 | M = N | |
| 5 | 24 | 1 ≤ N ≤ 105 | 1 ≤ M ≤ N | 1-4 |
Пояснения к примерам
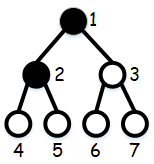
В первом примере в первое прохождение можно пройти уровни (1, 3, 6), во второе прохождение — (1, 3, 7), в третье прохождение (1, 2, 4), в четвертое прохождение — (2, 5). Последнее прохождение можно начать со 2-о уровня, так как он уже был пройден и на нём можно было сохраниться. Всего для полного прохождения пришлось пройти 11 уровней.
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|
| 2 | |
|
| 3 | |
|
Разбор
Полное решение
Заведём граф g. Запустим DFS (Depth-First-Search, "поиск в глубину") от вершины с номером 1. Будем идти "вглубь" дерева, запоминая за сколько вершин до этого мы встречали последнюю точку сохранения (путь d = расстояние от последней точки сохранения). При встрече новой точки сохранения будем прибавлять к ответу d и обнулять d. При встрече листа (вершины, у которой нет вершин-потомков) будем добавлять к ответу d + 1 (т.к. мы учитываем путь до листа + сам лист). В конце DFS выводим ответ.
Частичные решения
После DFS (для нахождения родителей всех вершин) можно было запускать подъём вверх от всех вершин, ища ближайшую точку сохранения; аналогично сработал бы и подъём от всех листьев. В худшем случае это даёт асимптотику O(N2), что проходит подзадачи 1-2.
Также стоило обратить внимание на ограничения подзадач 3 и 4. В случае M = 1 только в 1-ой вершине можно сохраняться, а значит достаточно было подсчитать сумму "высот" всех листьев (т.е. расстояние от листа до вершины 1, учитывая, что вершину 1 нам придётся для каждого листа проходить заново). Сложность алгоритма составит O(N), но работать решение будет только для M = 1. Проходит подзадачу 3.
В случае M = N во всех вершинах можно сохраняться, а значит достаточно было подсчитать сумму рёбер, добавив на всех "развилках" (вершинах с cnt = 2 и более сыновей) cnt − 1 к ответу, т.к. нам придётся заново начинать с данной вершины, чтобы пойти к другим сыновьям. Сложность алгоритма составит O(N), но работать решение будет только для M = N. Проходит подзадачу 4.
| Подзадача | Дополнительные ограничения | Оценка времени работы решения | |
|---|---|---|---|
| N | M | ||
| 1 | 1 ≤ N ≤ 102 | 1 ≤ M ≤ N | O(N3) — Какой-нибудь кубический алгоритм |
| 2 | 1 ≤ N ≤ 104 | 1 ≤ M ≤ N | O(N2) — DFS с подъёмом от всех листьев |
| O(N2) — DFS с подъёмом от всех вершин | |||
| 3 | 1 ≤ N ≤ 105 | M = 1 | O(N) (только при M = 1) — DFS с подсчётом суммы высот листьев |
| 4 | 1 ≤ N ≤ 105 | M = N | O(N) (только при M = N) — DFS с подсчётом суммы рёбер |
| 5 | 1 ≤ N ≤ 105 | 1 ≤ M ≤ N | O(N) — DFS с запоминанием последней вершины с возможностью сохранения |