Задача D. Рыболовная сеть ≡
| Автор: | А. Усманов | Ограничение времени: | 2 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 256 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
Дедушка Леонида — мастер по плетению рыболовных сетей. Для создания таких сетей требуется обладать должным талантом и терпением. Настоящие мастера плели свои сети очень прочными, используя при этом ровно одну цельную верёвку.
Сеть представляет N узлов, соединённых между собой M рёбрами. Будем считать, что сеть могла быть сплетена одной цельной верёвкой, если существует непрерывный путь, проходящий через каждое ребро ровно по одному разу. Путь должен начинаться и заканчиваться в узлах.
Леонид нашел на чердаке рыболовную сеть своего дедушки. Ему стало интересно, могла ли быть сплетена эта сеть ровно из одной цельной верёвки.
Требуется написать программу, которая считывает описание сети, и определяет, могла ли эта сеть быть сплетена ровно из одной цельной верёвки.
Формат входных данных
Первая строка содержит два целых числа N и M — количество узлов и рёбер у рыболовной сети соответственно.
Далее идёт M строк, в каждой из которых записано два целых числа ui и vi — номера узлов, между которыми проходит i-е ребро.
Гарантируется, что у каждого узла есть хотя бы одно ребро.
Обратите внимание, что у сети могут быть петли и кратные рёбра.
Пояснение
Петлёй называется ребро, соединяющее узел с самим собой.
Кратные ребра — два и более рёбер, соединяющих одну и ту же пару узлов.
Формат выходных данных
В единственной строке выведите "Yes" или "No" (без кавычек) — могла ли данная сеть быть сплетена ровно из одной цельной верёвки.
Ограничения
1 ≤ N ≤ 105
1 ≤ M ≤ 2 ⋅ 105
1 ≤ ui, vi ≤ N
Описание подзадач и системы оценивания
Баллы за каждую подзадачу начисляются только в случае, если все тесты этой подзадачи и необходимых подзадач успешно пройдены.
Проверка каждой подзадачи выполняется до первой ошибки на каком-нибудь тесте этой подзадачи.
По запросу сообщается результат окончательной проверки на каждом тесте.
| Подзадача | Баллы | Дополнительные ограничения | Необходимые подзадачи | |
|---|---|---|---|---|
| N | M | |||
| 1 | 18 | 1 ≤ N ≤ 10 | 1 ≤ M ≤ 10 | |
| 2 | 20 | 1 ≤ N ≤ 103 | 1 ≤ M ≤ 2 ⋅ 103 | 1 |
| 3 | 29 | 1 ≤ N ≤ 105 | M = N − 1 | |
| 4 | 33 | 1 ≤ N ≤ 105 | 1 ≤ M ≤ 2 ⋅ 105 | 1-3 |
Пояснение к примерам
Первая сеть могла быть сплетена следующим образом:
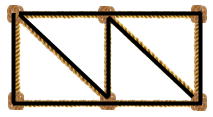
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|
| 2 | |
|
| 3 | |
|
| 4 | |
|
Разбор
Путь, описанный в задаче, также называется эйлеровым путём. Существует теорема, позволяющая быстро проверить наличие эйлерова пути в графе.
Теорема
Эйлеров путь существует тогда и только тогда, когда количество вершин с нечетным количеством рёбер равно нулю или двум.
Если количество вершин с нечетным количеством рёбер равно двум, то в одной из таких вершин путь должен начинаться, а в другой заканчиваться.
Если количество вершин с нечетным количеством рёбер равно нулю, то путь может начинаться в любой вершине, но должен закончиться в той же вершине, в которой начался.
Доказательство
Допустим, в графе несколько вершин с нечетным количеством рёбер. Путь, проходящий через любую вершину, занимает два ребра. Следовательно, рано или поздно количество неиспользованных рёбер у всех таких вершин станет равным единице. Значит, путь должен закончится в одной из таких вершин, так как попав в одну из них, выйти уже не получится. Следовательно, таких вершин не может быть больше двух: в одной путь начинается, в другой заканчивается.
Полное решение
Для полного решения задачи достаточно проверить наличие эйлерова пути в графе описанным способом: должно быть не более двух вершин с нечетным количеством рёбер.
Стоит отметить, что так же требовалось проверить граф на связность каким-нибудь методом обхода графа, например, поиском в глубину или ширину.
Частичные решения
Ограничения первой подзадачи позволяют перебрать все возможные варианты пути, например, с помощью рекурсивной функции.
Вторая подзадача подразумевает квадратичное решение с поиском эйлерова пути в графе.
В третьей подзадаче граф либо будет несвязным, либо является деревом. Есть только один способ представить дерево, имеющее эйлеров путь — в виде цепочки вершин. В такой цепочке у двух вершин будет по одному ребру, у остальных — по два.
| Подзадача | Дополнительные ограничения | Оценка времени работы решения | |
|---|---|---|---|
| N | M | ||
| 1 | 1 ≤ N ≤ 10 | 1 ≤ M ≤ 10 | O(N ⋅ M!) — перебор всех вариантов пути |
| 2 | 1 ≤ N ≤ 103 | 1 ≤ M ≤ 2 ⋅ 103 | O((N + M)2) — построение эйлерова пути |
| 3 | 1 ≤ N ≤ 105 | M = N − 1 | O(N + M) — проверка дерева на связность и подсчет количества листов |
| 4 | 1 ≤ N ≤ 105 | 1 ≤ M ≤ 2 ⋅ 105 | O(N + M) — проверка графа на связность и подсчет вершин с нечетным числом рёбер |