Problem E. Equidistant shell ≡
| Author: | A. Baranov | Time limit: | 1 sec | |
| Input file: | Standard input | Memory limit: | 256 Mb | |
| Output file: | Standard output |
Statement
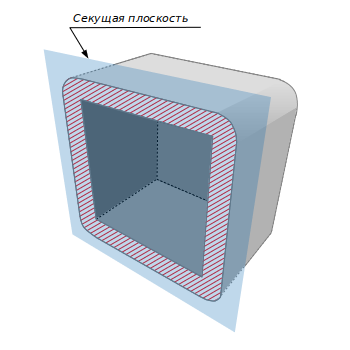
The equidistant shell of a three-dimensional body is the set of points external to it, within a distance of no more than a given δ. Example of equidistant shell of cube with its cross section is presented on picture.
Given an arbitrary convex polyhedron and a value of δ. You program must calculate volume of the equidistant shell.
Input format
Input data contains original polyhedron presented in a following format.
First there is the integer V, followed by exactly 3⋅V real numbers that are coordinates of the vertices.
Next, integer E, followed by exactly 2⋅E numbers of the vertices, defining the edges pairwise.
Next is the integer F, followed by exactly F faces represented in the following format.
First integer number of edges N, followed by N indices of edges of this face in an arbitrary order.
Indices of the all elements start from zero.
The floating point value of δ is written at the end of the input data.
Output format
Output data must contain the volume with an accuracy of at least 5 digits after decimal point.
Constraints
All faces are non-degenerate and convex.
Vertex coordinates are in the range from −10 to 10.
Count of elements of each kind does not exceed 100.
0≤δ≤1
Sample tests
| No. | Standard input | Standard output |
|---|---|---|
| 1 | |
|