Problem E. Enclosed by curves ≡
| Author: | A. Baranov | Time limit: | 1 sec | |
| Input file: | Standard input | Memory limit: | 512 Mb | |
| Output file: | Standard output |
Statement
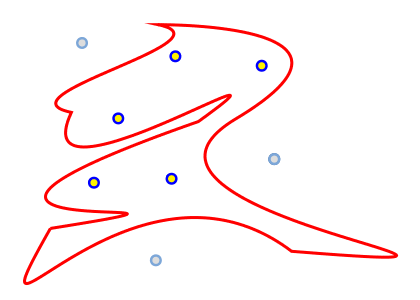
Novice programmer Vasya develops his own vector graphics editor. In addition to the usual primitives (like rectangles, circles, straight lines) his editor also supports working with objects of complex shapes, which are described using spline curves.
Each such curve consists of several pieces, in sequence one after the other, each of which is given by a parametric equation of the following form:
Xi(t)=AXi⋅t3+BXi⋅t2+CXi⋅t+DXi;
Yi(t)=AYi⋅t3+BYi⋅t2+CYi⋅t+DYi,
where t — scalar parameter, changing in range of [0,1].
Vasya uses closed spline curves to describe complex shapes. One of his tasks is to determine for every given point whether it lies inside such a figure.
Input format
The beginning of the input contains an integer N, followed by 8×N real numbers, specifying the coefficients of the corresponding splines
AXi, BXi, CXi, DXi,
AYi, BYi, CYi, DYi.
Next there is integer M, followed by 2×M real numbers, specifying the coordinates of the points (Xj,Yj).
Output format
Output must contain M integers (answers to each query):
1 — if the point is inside the contour,
0 — if it is outside.
Constraints
Within the specified accuracy, the contour is continuous and does not have self-intersections.
The distance from each point to the boundary of the contour is not less than 10−5.
The contour lies entirely within the rectangular area [−10,10]×[−10,10].
1≤N≤1000, 1≤M≤105.
Sample tests
| No. | Standard input | Standard output |
|---|---|---|
| 1 | |
|