Problem G. Geometric tomography ≡
| Author: | A. Baranov | Time limit: | 1 sec | |
| Input file: | Standard input | Memory limit: | 256 Mb | |
| Output file: | Standard output |
Statement
Flatlandian scientists investigate different geometric figures. However, due to limited perception, they can only work with one-dimensional projections of real objects. To simplify their life, they created a device that allows to make snapshots of an interesting to them object from different view sides. For the future research they need to develop a program that could restore two-dimensional figure from given snapshots.
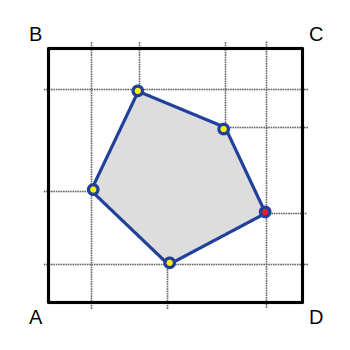
Let us consider some convex polygon nested into rectangle ABCD with sides parallel to the coordinate axes (see picture). Let us designate PAB, PBC, PCD, and PDA — snapshots represented by sets of vertices of the polygon that can be projected to the corresponding edge of the rectangle. There is also a single selected vertex that is marked on any snapshots that include it.
It is required to restore the coordinates of the vertices of the original polygon from the given set of snapshots with the selected vertex marked on them, where the point A is taken as an origin of coordinates.
Input format
Each line of input describes one of the sets PAB, PBC, PCD, and PDA, represented in the following format. First comes number N followed by N integers — projections of the vertices to the corresponding edge. Following is the index of the selected vertex in the current set, or − 1 if there is no selected vertex in the current set.
Vertices in each separate set are numbered from zero in clockwise order.
Output format
Output must contain coordinates of the vertices of the polygon in clockwise order starting from the selected vertex.
Constraints
It is guaranteed that the polygon is not degenerate (i.e. its area is not zero) and any two its vertices do not coincide.
Number of the vertices of the polygon does not exceed 2 ⋅ 105, their coordinates are in range from 0 to 109.
Sample tests
| No. | Standard input | Standard output |
|---|---|---|
| 1 | |
|
| 2 | |
|