Problem B. Binary Operation ≡
| Author: | ACM ICPC NEERC 2010 Jury | Time limit: | 2 sec | |
| Input file: | binary.in | Memory limit: | 256 Mb | |
| Output file: | binary.out |
Statement
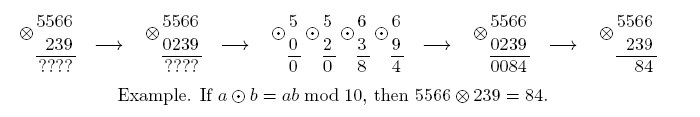 Consider a binary operation op defined on digits 0 to 9, op: digs × digs ↦ digs, such that 0op 0 = 0.
Consider a binary operation op defined on digits 0 to 9, op: digs × digs ↦ digs, such that 0op 0 = 0.
A binary operation opd is a generalization of op to the set of non-negative integers, opd: nneg × nneg ↦ nneg. The result of aopd b is defined in the following way: if one of the numbers a and b has fewer digits than the other in decimal notation, then append leading zeroes to it, so that the numbers are of the same length; then apply the operation op digit-wise to the corresponding digits of a and b.
Let us define opd to be left-associative, that is, aopd bopd c is to be interpreted as (aopd b)opd c.
Given a binary operation op and two non-negative integers a and b, calculate the value of res.
Input file format
The first ten lines of the input file contain the description of the binary operation op. The i-th line of the input file contains a space-separated list of ten digits — the j-th digit in this list is equal to (i − 1)op (j − 1).
The first digit in the first line is always 0.
The eleventh line of the input file contains two non-negative integers a and b (0 ≤ a ≤ b ≤ 1018).
Output file format
Output a single number — the value of res without extra leading zeroes.
Sample tests
| No. | Input file (binary.in) |
Output file (binary.out) |
|---|---|---|
| 1 | |
|