Задача 4. Антенна ≡
| Автор: | Даниил Орешников, Геннадий Короткевич | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 512 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
Для связи с Землёй членам экспедиции на Марс необходимо собрать антенну. Антенна в разобранном состоянии представляет собой n фрагментов, i-й фрагмент представляет собой штангу длиной si сантиметров, на которой закреплены mi перекладин. Каждый фрагмент содержит хотя бы одну перекладину.
У каждой штанги есть начало, в котором расположен штекер, и конец, в котором расположено гнездо. Любые две штанги можно последовательно соединить, присоединив начало одной к концу другой. Для каждой перекладины известно расстояние от начала её штанги в сантиметрах. Для i-го фрагмента это расстояние может быть от 0 до si, значение 0 означает, что перекладина находится непосредственно в начале штанги, значение si — что она находится непосредственно в конце штанги. Толщиной перекладин и размерами штекера и гнезда следует пренебречь.
На рисунке показаны три фрагмента антенны из первого примера и отмечены расстояния от начала штанги до перекладины.

Чтобы корректно собрать антенну, необходимо соединить в некотором порядке все n фрагментов, при этом расстояние между любыми двумя соседними перекладинами должно быть одинаковым.
На рисунке показан корректный способ соединить фрагменты в первом примере.

К сожалению, члены экспедиции забыли инструкцию по сборке антенны на Земле, а передать её на Марс не представляется возможным — ведь антенна ещё не собрана. Помогите исследователям!
Требуется определить, в каком порядке необходимо соединить фрагменты антенны, чтобы установить связь с Землей.
Формат входных данных
В первой строке дано одно число n — количество фрагментов.
Далее дано описание n фрагментов. В первой строке описания фрагмента даны два целых числа mi и si — количество перекладин и длина штанги в i-м фрагменте. В следующей строке даны mi целых чисел pi, j — позиции перекладин, pi, j равно расстоянию в сантиметрах от начала штанги до j-й перекладины на ней.
Формат выходных данных
Если собрать антенну указанным образом возможно,
в первой строке выведите Yes,
а во второй строке выведите перестановку чисел от 1 до n —
номера фрагментов в порядке, в котором их следует соединить,
начало каждого следующего фрагмента в этом порядке присоединяется
к концу предыдущего фрагмента.
Если существует несколько подходящих ответов, можно вывести любой из них.
Если собрать антенну невозможно, в единственной строке выведите No.
Ограничения
1 ≤ n ≤ 100 000, 1 ≤ mi ≤ 100 000, 0 ≤ si ≤ 109
0 ≤ pi, 1 < pi, 2 < … < pi, mi ≤ si
Сумма всех mi не превышает 100 000.
Система оценки
Баллы за каждую подзадачу начисляются только в случае, если все тесты для этой подзадачи и необходимых подзадач успешно пройдены.
| Подзадача | Баллы | Доп. ограничения | Необходимые подзадачи | Информация о проверке |
|---|---|---|---|---|
| 1 | 8 | n ≤ 8, mi = 1, si ≤ 100 | первая ошибка | |
| 2 | 8 | n ≤ 8, si ≤ 100 | 1 | первая ошибка |
| 3 | 21 | n ≤ 1 000 | 1, 2 | первая ошибка |
| 4 | 21 | ∑mi > n | первая ошибка | |
| 5 | 21 | si ≤ 100 | 1, 2 | первая ошибка |
| 6 | 21 | нет | 1 — 5 | первая ошибка |
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|
| 2 | |
|
| 3 | |
|
| 4 | |
|
| 5 | |
|
Разбор
Подзадача 1
Для того, чтобы решить первую подзадачу, можно перебрать, в каком порядке нужно соединить фрагменты. Всего существует n! таких вариантов. Для каждого варианта можно вычислить позиции всех перекладин и проверить, подходит ли такой вариант.
Подзадача 2
Для того, чтобы решить вторую подзадачу, нужно заметить, что если на одном из фрагментов присутствует более одной перекладины, то, если существует способ правильно собрать антенну, расстояние между соседними перекладинами должно быть равно расстоянию между перекладинами на этом фрагменте. Поэтому можно заранее проверить, что расстояния между соседними перекладинами в каждом отдельно взятом фрагменте равны. После чего можно оставить в каждом фрагменте только первую и последнюю перекладины. Затем, как в предыдущей подзадаче, перебрать порядок фрагментов и проверить, подходит ли он.
Общая идея
Как во второй подзадаче, оставим на каждом фрагменте только первую и последнюю перекладины. Пусть на i-м фрагменте первая перекладина находится на расстоянии li от начала, а последняя — на расстоянии ri от конца. Научимся проверять, существует ли порядок фрагментов, при котором расстояние между соседними перекладинами будет равно d. Пусть такой порядок существует, обозначим его q1, q2, …, qn. Тогда должно выполняться rqi + lqi + 1 = d (1 ≤ i ≤ n − 1), значит lqi + 1 = d − rqi. Рассмотрим граф, вершинами которого являются все целые числа. Проведем ориентированное ребро из li в d − ri для всех i. Заметим, что искомый порядок существует тогда и только тогда, когда в построенном графе существует Эйлеров путь. Поиск Эйлерова пути (и проверка существования) является стандартным алгоритмом.
Например, в первом тесте из примеров, l1 = 3, r1 = 4, l2 = 6, r2 = 2, l3 = 1, r3 = 2. В ответе на тест, d = 5. Построим граф по этим данным:
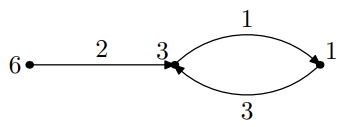
Рядом с вершинами написаны соответствующие им числа, а рядом с ребрами — номера соответствующих им фрагментов. Видно, что последовательность ребер 2, 1, 3 является Эйлеровым путем.
Для решения оставшихся подзадач, мы будем находить некоторое множество значений d, каждое из которых будем проверять за линейное время алгоритмом из предыдущего абзаца.
Подзадача 4
Чтобы решить четвертую подзадачу, нужно заметить, что по принципу Дирихле всегда будет существовать хотя бы один фрагмент, содержащий хотя бы две перекладины. Поэтому, если искомый порядок существует, расстояние d между соседними перекладинами должно быть равно расстоянию между соседними перекладинами на этом фрагменте. Воспользуемся алгоритмом и проверим, подходит ли данное d.
Подзадача 3
Чтобы решить третью подзадачу, можно перебрать два варианта:
- Если фрагмент номер 1 не будет стоять самым последним, то можно перебрать номер фрагмента i, который будет стоять сразу после фрагмента 1, и проверить d = r1 + li.
- Если фрагмент номер 1 будет стоять самым последним, то фрагмент номер 2 не будет стоять последним. Можно перебрать номер фрагмента i, который будет стоять после фрагмента 2, и проверить d = r2 + li.
Таким образом, мы проверим O(n) вариантов, каждый за время O(n). Итого, решение работает за O(n2).
Подзадача 5
Чтобы решить пятую подзадачу, можно проверить все значения d от 0 до 200. Дополнительно ускорить решение можно, проверяя только значения d от 0 до ⌊100 ⋅ nn − 1⌋.
Подзадача 6
Наконец, чтобы решить задачу на полный балл, нужно было научиться проверять только O(1) различных вариантов d. Рассмотрим пары (lqi, rqi + 1) и отсортируем их в порядке возрастания l. Заметим, что так как суммы значений в каждой паре равны, значения r будут убывать. Среди всех значений l в рассмотренных парах не присутствует ровно одно, соответствующее первому фрагменту. Аналогично, среди всех значений r отсутствует значение, соответствующее последнему фрагменту. Таким образом, можно отсортировать все значения l в порядке возрастания, все значения r в порядке убывания и проверить 4 варианта значения d: сумма одного из двух минимальных значений l и одного из двух максимальных значений r.